题目内容
3.已知x,y满足$\frac{axy}{bx+cy}$=1,$\frac{axy}{cx-by}$=2(b≠3c,c≠-2b),求$\frac{y}{x}$的值.分析 化简两式得出bx+cy=2cx-2by,即可得出$\frac{y}{x}$的值.
解答 解:∵$\frac{axy}{bx+cy}$=1,得axy=bx+cy,$\frac{axy}{cx-by}$=2,得axy=2cx-2by,
∴bx+cy=2cx-2by,即(c+2b)y=(2c-b)x,
∴$\frac{y}{x}$=$\frac{2c-b}{c+2b}$.
点评 本题主要考查了分式的混合运算,解题的关键是正确的化简.

练习册系列答案
相关题目
15.关于x的方程2x2-8x-p=0有一个正根,一个负根,则p的值是( )
| A. | 0 | B. | 正数 | C. | -8 | D. | -4 |
 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.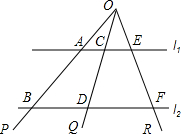 如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.
如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.