题目内容
16.为了贯彻落实双城区区委政府提出的“精准扶贫”政策,某部门制定了一系列关于帮扶甲、乙两贫困村的计划,现决定为这两个村配备一些电脑支持村民开展“农村淘宝”服务,已知某商店销售10台A型电脑和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y与x的函数关系式;
②该商店购进A型,B型各多少台,才能使销售利润最大?
分析 (1)设每台A型电脑销售利润为x元,每台B型电脑的销售利润为y元,然后根据利润4000元和3500元列出方程组,然后求解即可;
(2)①根据总利润等于两种电脑的利润之和列式整理即可得解;
②根据B型电脑的进货量不超过A型电脑的2倍列不等式求出x的取值范围,然后根据一次函数的增减性求出利润的最大值即可.
解答 解:(1)设每台A型电脑销售利润为x元,每台B型电脑的销售利润为y元,
根据题意得$\left\{\begin{array}{l}{10x+20y=4000}\\{20x+10y=3500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=150}\end{array}\right.$.
答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元;
(2)①据题意得,y=100x+150(100-x),
即y=-50x+15000,
②据题意得,100-x≤2x,
解得x≥33$\frac{1}{3}$,
∵y=-50x+15000中,k=-50<0,
∴y随x的增大而减小,
∵x为正整数,
∴当x=34时,y取最大值,则100-x=66,
答:商店购进34台A型电脑和66台B型电脑,才能使销售利润最大.
点评 本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式,读懂题目信息,准确找出等量关系列出方程组是解题的关键,利用一次函数的增减性求最值是常用的方法.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.若关于x的不等式组$\left\{\begin{array}{l}{x-a>2}\\{b-2x>0}\end{array}\right.$的解集为-1<x<1,则(a+b)2017的值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
1.河北省积极响应国家号召,2017年将压减钢铁产能3186万吨,是全国压减钢铁产能目标的六成多,将3186用科学记数法表示为( )
| A. | 3.186×103 | B. | 3.186×104 | C. | 31.86×102 | D. | 0.3186×104 |
8. 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )| A. | ∠1=∠2 | B. | ∠BAD=∠BCD | C. | AO=CO | D. | AC⊥BD |
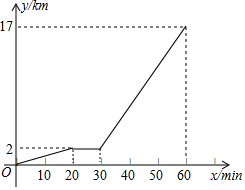 星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:
星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题: