题目内容
8.先化简再求值:(1)(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$,其中x=2;
(2)$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$÷$\frac{x+2}{x+1}$-$\frac{x}{x-2}$,其中x=2-$\sqrt{2}$.
分析 (1)首先计算小括号里面的减法,然后再计算除法,将分式化简;最后把x=2代入化简后的算式,求出算式的值是多少即可.
(2)首先计算除法,然后再计算减法,将分式化简;最后把x=2-$\sqrt{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$
=$\frac{x+1}{x+2}$÷$\frac{{x}^{2}-1}{x+2}$
=$\frac{1}{x-1}$
当x=2时,
原式=$\frac{1}{x-1}$=$\frac{1}{2-1}=1$.
(2)$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$÷$\frac{x+2}{x+1}$-$\frac{x}{x-2}$
=$\frac{(x+2)(x-2)}{{(x-2)}^{2}}$÷$\frac{x+2}{x+1}$-$\frac{x}{x-2}$
=$\frac{x+1}{x-2}$-$\frac{x}{x-2}$,
=$\frac{1}{x-2}$
当x=2-$\sqrt{2}$时,
原式=$\frac{1}{x-2}=\frac{1}{2-\sqrt{2}-2}=-\frac{\sqrt{2}}{2}$.
点评 此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤,解答此题的关键是要明确:代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
16.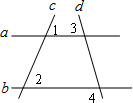 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )| A. | 35° | B. | 70° | C. | 90° | D. | 110° |
3. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )
 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )| A. | 西偏北30° | B. | 北偏西60° | C. | 北偏东30° | D. | 东偏北60° |
13.若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax+b=2有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系为( )
| A. | p<m<n<q | B. | m<p<q<n | C. | m<p<n<q | D. | p<m<q<n |
18.某次活动课上,要在某个小组中随机挑选2名同学上台表演,已知这个小组共有2名男同学,2名女同学,那么恰好挑选1名男同学和1名女同学的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |