题目内容
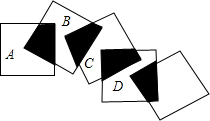如图，五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是这四个正方形的对角线的交点，请利用上题的结论，求图中四块阴影面积的总和是多少？考点：中心对称
专题：
分析：根据正方形的中心对称性，每一个阴影部分的面积等于正方形面积的
，四块阴影面积的总和正好等于一个正方形的面积，然后列式计算即可得解．
| 1 |
| 4 |
解答：解：由正方形的性质得，一个阴影部分的面积等于正方形的面积的
，
所以，四块阴影面积的总和正好等于一个正方形的面积，
∵五个正方形的边长都为2cm，
∴四块阴影面积的总和=22=4（cm2）．
| 1 |
| 4 |
所以，四块阴影面积的总和正好等于一个正方形的面积，
∵五个正方形的边长都为2cm，
∴四块阴影面积的总和=22=4（cm2）．
点评：本题考查了正方形的性质，熟记中心对称性判断出每一个阴影部分的面积等于正方形的面积的
是解题的关键．
| 1 |
| 4 |
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，AB=AC，点D是BC的中点，点E在AD上，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°．