题目内容
 在△ABC中,AB=AC,点D是BC的中点,点E在AD上,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°.
在△ABC中,AB=AC,点D是BC的中点,点E在AD上,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°.求证:△AEF≌△BCF.
考点:全等三角形的判定
专题:证明题
分析:根据垂直定义求出∠AFB=∠BFC=∠ADB=90°,求出∠CBF=∠EAF,根据等腰三角形的判定推出AF=BF,根据ASA推出两三角形全等即可.
解答:证明:∵AD⊥BC,BF⊥AC,
∴∠AFB=∠BFC=∠ADB=90°,
∴∠C+∠CBF=90°,∠C+∠EAF=90°,
∴∠CBF=∠EAF,
∵∠AFB=90°,∠BAC=45°,
∴∠ABF=∠BAF=45°,
∴AF=BF,
在△AEF和△BCF中,
,
∴△AEF≌△BCF(SAS).
∴∠AFB=∠BFC=∠ADB=90°,
∴∠C+∠CBF=90°,∠C+∠EAF=90°,
∴∠CBF=∠EAF,
∵∠AFB=90°,∠BAC=45°,
∴∠ABF=∠BAF=45°,
∴AF=BF,
在△AEF和△BCF中,
|
∴△AEF≌△BCF(SAS).
点评:本题考查了对全等三角形的判定定理,三角形内角和定理,垂直定义的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
如果一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
| A、十边形 | B、十一边形 |
| C、十二边形 | D、十三边形 |
有下列说法:①等腰三角形的顶角平分线与此角所对边上的高重合;②等腰三角形的底角一定是锐角;③等腰三角形的一边不可能是另一边的两倍;④底角相等的两个等腰三角形的面积相等.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列结论正确的是( )
| A、有理数包括正数和负数 |
| B、数轴上原点两侧的数互为相反数 |
| C、0是最小的整数 |
| D、无限不循环小数叫做无理数 |
已知a=
-1,b=
-2,c=2
-
,那么a、b、c的大小关系是( )
| 2 |
| 6 |
| 2 |
| 6 |
| A、a<b<c |
| B、c<b<a |
| C、.b<a<c |
| D、.c<a<b |
当y=-1时,则代数式-y3-y2+y-1的值为( )
| A、-4 | B、-3 | C、-2 | D、-1 |
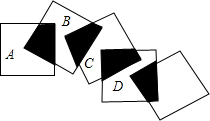 如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?
如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?