题目内容
在△ABC中，∠C=90°，∠A、∠B、∠C的对应边分别是a、b、c，且3a=
b，则∠B= ，sinB= ．
| 3 |
考点：解直角三角形
专题：
分析：先由3a=
b，得出b=
a．然后在△ABC中，根据正切函数的定义得出tanB=
=
，由特殊角的三角函数值可知∠B=60°，再根据60°的正弦函数值即可求出sinB．
| 3 |
| 3 |
| b |
| a |
| 3 |
解答：解：∵3a=
b，
∴b=
a．
在△ABC中，∵∠C=90°，
∴tanB=
=
=
，
∴∠B=60°，
∴sinB=sin60°=
．
故答案为60°，
．
| 3 |
∴b=
| 3 |
在△ABC中，∵∠C=90°，
∴tanB=
| b |
| a |
| ||
| a |
| 3 |
∴∠B=60°，
∴sinB=sin60°=
| ||
| 2 |
故答案为60°，
| ||
| 2 |
点评：本题考查了解直角三角形，牢记锐角三角函数的定义及特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
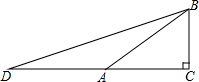已知：如图，Rt△ABC中，∠C=90°，∠BAC=30°，延长CA至D点，使AD=AB．
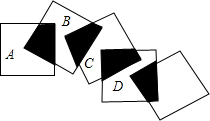如图，五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是这四个正方形的对角线的交点，请利用上题的结论，求图中四块阴影面积的总和是多少？
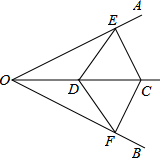如图，CD是∠AOB平分线上的点，CE⊥OA于点E，CF⊥OB于点F，求证：∠CDE=∠CDF．
已知四边形ABCD顶点都在4×4的正方形网格格点上，如图所示，