题目内容
已知关于x、y的方程2x2-y-3=0.
(1)请你直接写出该方程的两组整数解;
(2)若
和
是方程2x2-y-3=0的两组不同的解,求2m3-2mn+2n3的值.
(1)请你直接写出该方程的两组整数解;
(2)若
|
|
考点:高次方程
专题:
分析:(1)根据使方程成立的未知数的值是方程的解,可得答案;
(2)根据方程组的解满足方程,把方程的解代入方程,可得2m2-n-3=0,2n2-m-3=0,根据等式的性质,可得m+n=-
,根据等量代换,可得(n+3)•m-2mn+(m+3)•n,根据去括号、合并同类项,可得答案.
(2)根据方程组的解满足方程,把方程的解代入方程,可得2m2-n-3=0,2n2-m-3=0,根据等式的性质,可得m+n=-
| 1 |
| 2 |
解答:解:(1)
,
;
(2)∵
和
是方程2x2-y-3=0的两组不同的解,
∴2m2-n-3=0①,2n2-m-3=0②,
∴①-②得2(m2-n2)+m-n=0.
∴2(m+n)(m-n)+(m-n)=0.
∴(m-n)[2(m+n)+1]=0.
∵m≠n,
∴2(m+n)+1=0.
∴m+n=-
.
∵2m2=n+3,2n2=m+3,
∴2m3-2mn+2n3=2m2•m-2mn+2n2•n
=(n+3)•m-2mn+(m+3)•n
=mn+3m-2mn+mn+3n
=3(m+n)
=3×
=
.
|
|
(2)∵
|
|
∴2m2-n-3=0①,2n2-m-3=0②,
∴①-②得2(m2-n2)+m-n=0.
∴2(m+n)(m-n)+(m-n)=0.
∴(m-n)[2(m+n)+1]=0.
∵m≠n,
∴2(m+n)+1=0.
∴m+n=-
| 1 |
| 2 |
∵2m2=n+3,2n2=m+3,
∴2m3-2mn+2n3=2m2•m-2mn+2n2•n
=(n+3)•m-2mn+(m+3)•n
=mn+3m-2mn+mn+3n
=3(m+n)
=3×
| 1 |
| 2 |
=
| 3 |
| 2 |
点评:本题考查了高次方程,分解降次是解题关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
在平面直角坐标系中,已知点A(-1,2)和点B(-1,0),则直线AB( )
| A、平行于x轴 |
| B、平行于y轴 |
| C、与坐标轴有2个交点 |
| D、过原点 |

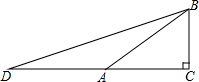 已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB.
已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB. 如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=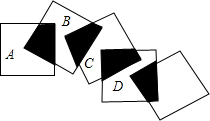 如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?
如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?