题目内容
点A、B的坐标分别为(-1,0)、(1,0),点C与点A、B构成等边三角形,点C的坐标为 (所有可能).
考点:等边三角形的判定,坐标与图形性质
专题:
分析:根据题意画出图形,求出边长AB=2,根据等边三角形的性质得出三边相等,再根据勾股定理求出OC,即可得出答案.
解答:解:
有两种情况:如图,∵点A、B的坐标分别为(-1,0)、(1,0),
∴OA=OB=1,AC1=AC2=AB=2,
由勾股定理得:OC1=OC2=
=
,
即点C的坐标是(0,
)或(0,-
),
故答案为:(0,
)或(0,-
).

有两种情况:如图,∵点A、B的坐标分别为(-1,0)、(1,0),
∴OA=OB=1,AC1=AC2=AB=2,
由勾股定理得:OC1=OC2=
| 22-12 |
| 3 |
即点C的坐标是(0,
| 3 |
| 3 |
故答案为:(0,
| 3 |
| 3 |
点评:本题考查了等边三角形的性质,勾股定理的应用,解此题的关键是能求出符合条件的所有情况.

练习册系列答案
相关题目
在平面直角坐标系中,已知点A(-1,2)和点B(-1,0),则直线AB( )
| A、平行于x轴 |
| B、平行于y轴 |
| C、与坐标轴有2个交点 |
| D、过原点 |
下列结论正确的是( )
| A、有理数包括正数和负数 |
| B、数轴上原点两侧的数互为相反数 |
| C、0是最小的整数 |
| D、无限不循环小数叫做无理数 |
 如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=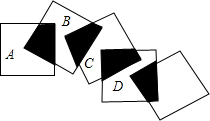 如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?
如图,五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,请利用上题的结论,求图中四块阴影面积的总和是多少?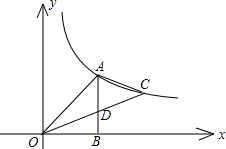 已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=