题目内容
如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC关于y轴翻折后得到△A2B2C,画出△A2B2C2的图形并写出点B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,画出△AB3C3.

(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC关于y轴翻折后得到△A2B2C,画出△A2B2C2的图形并写出点B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,画出△AB3C3.

考点:作图-位似变换,作图-轴对称变换,作图-平移变换
专题:
分析:(1)利用平移的性质得出对应点位置进而得出答案;
(2)利用轴对称的性质得出对应点位置进而得出答案;
(3)利用位似变换的性质得出对应点位置进而得出答案.
(2)利用轴对称的性质得出对应点位置进而得出答案;
(3)利用位似变换的性质得出对应点位置进而得出答案.
解答: 解:(1)如图所示:△A1B1C1即为所求,点B1的坐标为:(-9,0);
解:(1)如图所示:△A1B1C1即为所求,点B1的坐标为:(-9,0);
(2)如图所示:△A2B2C2即为所求,点B2的坐标为:(-5,0);
(3)如图所示:△AB3C3即为所求.
 解:(1)如图所示:△A1B1C1即为所求,点B1的坐标为:(-9,0);
解:(1)如图所示:△A1B1C1即为所求,点B1的坐标为:(-9,0);(2)如图所示:△A2B2C2即为所求,点B2的坐标为:(-5,0);
(3)如图所示:△AB3C3即为所求.
点评:此题主要考查了平移变换以及轴对称变换和位似变换等知识,正确得出对应点坐标位置是解题关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB于点M,下列结论不一定成立的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点M,下列结论不一定成立的是( )| A、CM=DM | ||||
B、
| ||||
| C、∠BOD=2∠A | ||||
| D、OM=MB |
 如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为( )
如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为( )| A、2:1 | B、4:1 |
| C、3:1 | D、5:3 |
 如图,在直线上有A、B、C、D四个点,且BC=2AB=3CD,若AD=11,那么CD=( )
如图,在直线上有A、B、C、D四个点,且BC=2AB=3CD,若AD=11,那么CD=( )| A、2 | B、3 | C、6 | D、9 |

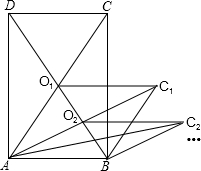 如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2 ,…,依此类推,则平行 四边形ABC2013O2013的面积为( )
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2 ,…,依此类推,则平行 四边形ABC2013O2013的面积为( ) 如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与8O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;
如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与8O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;