题目内容
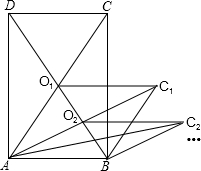 如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2 ,…,依此类推,则平行 四边形ABC2013O2013的面积为( )
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2 ,…,依此类推,则平行 四边形ABC2013O2013的面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:矩形的性质,平行四边形的性质
专题:规律型
分析:因为矩形的对边和平行四边形的对边互相平行,且矩形的对角线和平行四边形的对角线都互相平分,所以上下两平行线间的距离相等,平行四边形的面积等于底×高,所以第一个平行四边形是矩形的一半,第二个平行四边形是第一个平行四边形的一半依次可推下去.
解答:解:∵DO1=BO1,DC∥O1C1∥AB,
∴夹在DC和O1C1,O1C1和AB之间的距离相等,
∴第一个平行四边形的面积是矩形面积的一半,
依此类推第二个平行四边形是第一个平行四边形面积的一半,
所以第2013个平行四边形的面积为:5×(
)2013=
,
故选C.
∴夹在DC和O1C1,O1C1和AB之间的距离相等,
∴第一个平行四边形的面积是矩形面积的一半,
依此类推第二个平行四边形是第一个平行四边形面积的一半,
所以第2013个平行四边形的面积为:5×(
| 1 |
| 2 |
| 5 |
| 22013 |
故选C.
点评:本题考查了矩形的性质和平行四边形的性质的应用,解此题的关键是能根据求出的结果得出规律,注意:矩形的对角线相等且互相平分,平行四边形的对角线互相平分,矩形和平行四边形的对边平行.

练习册系列答案
相关题目
下列调查方式中最适合的是( )
| A、要了解一批节能灯的使用寿命,采用全面调查方式 |
| B、调查你所在班级的同学的身高,采用抽样调查方式 |
| C、环保部门调查嘉陵江某段水域的水质情况,采用抽样调查方式 |
| D、调查全市中学生每天的就寝时间,采用全面调查方式 |
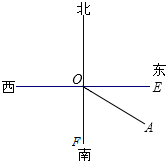 如图,货轮D在航行过程中,发现灯塔A在它的南偏东60°的方向上.同时,在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C.
如图,货轮D在航行过程中,发现灯塔A在它的南偏东60°的方向上.同时,在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C.
 如图,在边长为1的小正方形组成的12×12网格中,△ABC在直线MN的上方,其三个顶点A、B、C分别在网格的格点上,将△ABC沿直线MN翻折.
如图,在边长为1的小正方形组成的12×12网格中,△ABC在直线MN的上方,其三个顶点A、B、C分别在网格的格点上,将△ABC沿直线MN翻折. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )