题目内容

4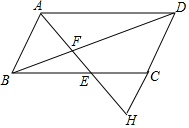．如图，点H在平行四边形ABCD的边DC延长线上，连结AH分别交BC、BD于点E、F．求证：$\frac{BE}{AD}$=$\frac{AB}{DH}$．

分析 先根据平行四边形的性质得出AB∥DC，∠ABE=∠ADH，故可得出∠BAE=∠H，由此可得出△ABE∽△HDA，据此可得出结论．

解答 证明：∵四边形ABCD是平行四边形，
∴AB∥DC，∠ABE=∠ADH，
∴∠BAE=∠H，
∴△ABE∽△HDA，
∴$\frac{BE}{AD}$=$\frac{AB}{DH}$．

点评 本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．

练习册系列答案
相关题目
14．尺规作图（不写作法，保留作图痕迹）
如图，已知△ABC，求作△ABC的高AD．
15．已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD=60°，△CBD是等边三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有④．（只填序号）
①2个 ②3个 ③4个 ④4个以上
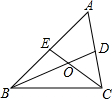12．已知：如图，△ABC的中线BD、CE交于点O．
（1）求证：$\frac{OD}{OB}$=$\frac{1}{2}$；
（2）求证：△ABC的三条中线交于一点．
19．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．
原题：如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：$\frac{DP}{BQ}$=$\frac{PE}{QC}$．
（1）尝试探究：在图1中，由DP∥BQ得△ADP∽△ABQ（填“≌”或“∽”），则$\frac{DP}{BQ}$=$\frac{AP}{AQ}$，同理可得$\frac{PE}{QC}$=$\frac{AP}{AQ}$，从而$\frac{DP}{BQ}$=$\frac{PE}{QC}$．
（2）类比延伸：如图2，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于M、N两点，若AB=AC=1，则MN的长为$\frac{\sqrt{2}}{9}$．
（3）拓展迁移：如图3，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交于DE于M、N两点，AB＜AC，求证：MN2=DM•EN．
9．计算：（1）-100÷10×（-$\frac{1}{10}$）2；（2）2.5÷[（$\frac{1}{5}$-1）×（2+$\frac{1}{2}$）]．
16．从2007年4月18日开始，我国铁路第六次提速，某次列车平均提速v km/h．
（1）若提速前列车的平均速度为x km/h，行驶1200km的路程，提速后比提速前少用多长时间？
（2）若v=50，行驶1200km的路程，提速后所用时间是提速前的$\frac{4}{5}$，求提速前列车的平均速度？
（3）用相同的时间，列车提速前行驶s km，提速后比提速前多行驶50km，则提速前的平均速度为$\frac{sv}{50}$km/h．
13．定义一种新运算“⊕”：a⊕b=2a-3b，
比如：1⊕（-3）=2×1-3×（-3）=11．
（1）求（-2）⊕3的值；
（2）若（3x-2）⊕（x+1）=2，求x的值．
18．某厂共有140名生产工人，每个工人每天可生产螺栓25个或螺母20个，如果一个螺栓与两个螺母配成一套，那么使每天生产出来的产品配成最多套，每天应安排40名工人生产螺栓，100名工人生产螺母．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网