题目内容
12.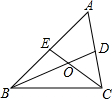 已知:如图,△ABC的中线BD、CE交于点O.
已知:如图,△ABC的中线BD、CE交于点O.(1)求证:$\frac{OD}{OB}$=$\frac{1}{2}$;
(2)求证:△ABC的三条中线交于一点.
分析 (1)根据三角形的重心的概念和性质证明;
(2)延长AO与BC相交于点F,过点B作BH∥CE交AO的延长线于H,连接CH,证明四边形BHCO是平行四边形,根据平行四边形的性质证明.
解答 证明:(1)∵△ABC的中线BD、CE交于点O,
∴点O是△ABC的重心,
∴$\frac{OD}{OB}$=$\frac{1}{2}$;
(2)如图,延长AO与BC相交于点F,过点B作BH∥CE交AO的延长线于H,连接CH,
∵CE是△ABC的中线,
∴O是AH的中点,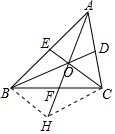
∵BD是△ABC的中线,
∴OD是△ACH的中位线,
∴OD∥CH,
∴四边形BHCO是平行四边形,
∴BF=CF,
∵AF是△ABC的中线,
即三条中线交于一点O.
点评 本题考查的是三角形的重心的概念和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
相关题目
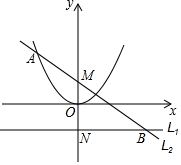 已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.
已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.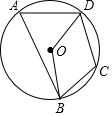 如图四边形ABCD的四个顶点在同一个圆上,这样的四边四边形叫做圆内接四边形.
如图四边形ABCD的四个顶点在同一个圆上,这样的四边四边形叫做圆内接四边形. 一个圆锥的三视图如图所示,求圆锥的全面积.
一个圆锥的三视图如图所示,求圆锥的全面积.
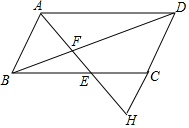 如图,点H在平行四边形ABCD的边DC延长线上,连结AH分别交BC、BD于点E、F.求证:$\frac{BE}{AD}$=$\frac{AB}{DH}$.
如图,点H在平行四边形ABCD的边DC延长线上,连结AH分别交BC、BD于点E、F.求证:$\frac{BE}{AD}$=$\frac{AB}{DH}$. 如图,在Rt△ABC中,∠A=90°,BE平分∠ABC,过点E作BC的垂线交BC于点D,CE=BE.求证:AB=CD.
如图,在Rt△ABC中,∠A=90°,BE平分∠ABC,过点E作BC的垂线交BC于点D,CE=BE.求证:AB=CD.