题目内容
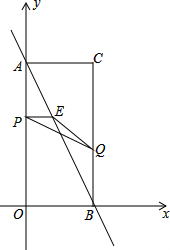 如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
考点:一次函数综合题,平行线的性质,三角形的面积,菱形的性质
专题:综合题
分析:(1)依据待定系数法即可求得;
(2)有两种情况:当0<t<2时,PF=4-2t,当2<t≤4时,PF=2t-4,然后根据面积公式即可求得;
(3)依据菱形的邻边相等关系即可求得.
(2)有两种情况:当0<t<2时,PF=4-2t,当2<t≤4时,PF=2t-4,然后根据面积公式即可求得;
(3)依据菱形的邻边相等关系即可求得.
解答:解:(1)∵C(2,4),
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴
,
解得
∴直线AB的解析式为y=-2x+4.
(2)如图2,过点Q作QF⊥y轴于F,
∵PE∥OB,
∴
=
=
∴有AP=BQ=t,PE=
t,AF=CQ=4-t,
当0<t<2时,PF=4-2t,
∴S=
PE•PF=
×
t(4-2t)=t-
t2,
即S=-
t2+t(0<t<2),
当2<t≤4时,PF=2t-4,
∴S=
PE•PF=
×
t(2t-4)=
t2-t(2<t≤4).
(3)t1=
,H1(
,
),
t2=20-8
,H2(10-4
,4).
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴
|
解得
|
∴直线AB的解析式为y=-2x+4.
(2)如图2,过点Q作QF⊥y轴于F,

∵PE∥OB,
∴
| PE |
| AP |
| OB |
| AO |
| 1 |
| 2 |
∴有AP=BQ=t,PE=
| 1 |
| 2 |
当0<t<2时,PF=4-2t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即S=-
| 1 |
| 2 |
当2<t≤4时,PF=2t-4,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)t1=
| 20 |
| 13 |
| 10 |
| 13 |
| 12 |
| 13 |
t2=20-8
| 5 |
| 5 |
点评:本题考查了待定系数法求解析式,平行线的性质,以及菱形的性质和三角形的面积公式的应用.

练习册系列答案
相关题目
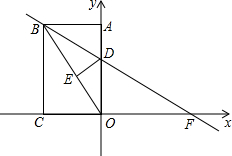 如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-12,16),矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-12,16),矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F. 以A、B、C为圆心的三个圆,半径均为r,其中1<r<2,每两个圆心间的距离都是2.若B′是⊙A和⊙C的交点且在⊙B外,C′是⊙A和⊙B的交点且在⊙C外,试求B′C′的长.
以A、B、C为圆心的三个圆,半径均为r,其中1<r<2,每两个圆心间的距离都是2.若B′是⊙A和⊙C的交点且在⊙B外,C′是⊙A和⊙B的交点且在⊙C外,试求B′C′的长.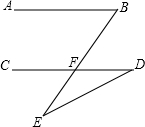 如图,已知:∠B=∠D+∠E,试说明:AB∥CD.
如图,已知:∠B=∠D+∠E,试说明:AB∥CD.