题目内容
8.解下列方程组.(1)$\left\{\begin{array}{l}x+y=1\\ y=2x+4\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+2y=13}\\{3x-2y=5}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=1①}\\{y=2x+4②}\end{array}\right.$,
把②代入①得:x+2x+4=1,
解得:x=-1,
把x=-1代入②得:y=2,
则方程组的解为$\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$;
(2)$\left\{\begin{array}{l}{3x+2y=13①}\\{3x-2y=5②}\end{array}\right.$,
①+②得:6x=18,
解得:x=3,
由①-②得:4y=8,
解得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图,AB∥CD,AD∥BC,∠A:∠B=2:3,则∠CDE=( )
如图,AB∥CD,AD∥BC,∠A:∠B=2:3,则∠CDE=( )
 如图,AB∥CD,AD∥BC,∠A:∠B=2:3,则∠CDE=( )
如图,AB∥CD,AD∥BC,∠A:∠B=2:3,则∠CDE=( )| A. | 60° | B. | 65° | C. | 72° | D. | 80° |
20. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )| A. | AD=BD | B. | BD=CD | C. | ∠A=∠BED | D. | ∠ECD=∠EDC |
9.如果受季节影响,某种原价为100元的商品降价a%出售,那么该商品的售价可表示为( )元.
| A. | $\frac{100}{1-a%}$ | B. | $\frac{100}{1+a%}$ | C. | 100(1-a%) | D. | 100(1+a%) |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,Rt△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3),请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,Rt△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3),请按要求完成下列步骤: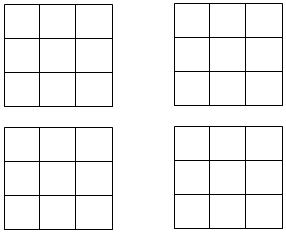 在如图所示的3×3的方格中,画出4个面积不小于1且小于9的不同的正方形,而且所画正方形的顶点都在方格的顶点上并直接写出所画正方形的面积.
在如图所示的3×3的方格中,画出4个面积不小于1且小于9的不同的正方形,而且所画正方形的顶点都在方格的顶点上并直接写出所画正方形的面积.
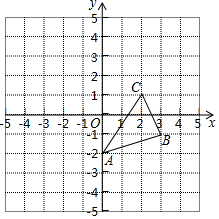 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).