题目内容
18．
如图，AB∥CD，AD∥BC，∠A：∠B=2：3，则∠CDE=（ ）| A． | 60° | B． | 65° | C． | 72° | D． | 80° |
分析 先根据平行线的性质，得出∠A=72°，再根据AB∥CD，即可得到∠CDE=∠A=72°．
解答 解：∵AD∥BC，
∴∠A+∠B=180°，
又∵∠A：∠B=2：3，
∴∠A=72°，
又∵AB∥CD，
∴∠CDE=∠A=72°，
故选：C．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补；两直线平行，同位角相等．
练习册系列答案
名校课堂系列答案
相关题目
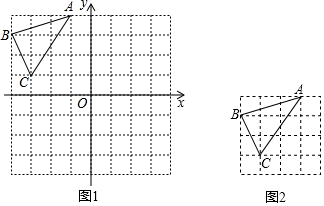
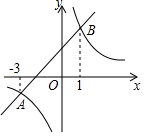如图，双曲线y=$\frac{m}{x}$（m≠0）和直线y=x+b交于A，B两点，其横坐标分别为-3，1，则m的值是（ ）
13．
如图，直线l1、l2与直线l3相交，若l1∥l2，∠1=120°，则∠2=（ ）
如图，直线l1、l2与直线l3相交，若l1∥l2，∠1=120°，则∠2=（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |
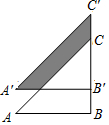如图，直角边长为3的等腰直角三角形ABC沿直角边BC所在直线向上平移1个单位，得到三角形A'B'C'，则阴影部分的面积为$\frac{5}{2}$．
10．若$\sqrt{a-3}$+（b+2）2=0，则点M（a，b）所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，已知线段AB，BC，∠ABC=90°