题目内容
12.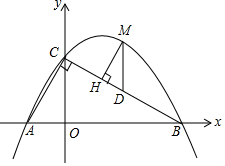 如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+$\sqrt{3}$经过A,B两点.
如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+$\sqrt{3}$经过A,B两点.(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
分析 (1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;
(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;
(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
解答 解:
(1)∵直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0,$\sqrt{3}$),
∴OB=3,OC=$\sqrt{3}$,
∴tan∠BCO=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠BCO=60°,
∵∠ACB=90°,
∴∠ACO=30°,
∴$\frac{AO}{CO}$=tan30°=$\frac{\sqrt{3}}{3}$,即$\frac{AO}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,解得AO=1,
∴A(-1,0);
(2)∵抛物线y=ax2+bx+$\sqrt{3}$经过A,B两点,
∴$\left\{\begin{array}{l}{a-b+\sqrt{3}=0}\\{9a+3b+\sqrt{3}=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$;
(3)∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH=$\frac{1}{2}$DM,MH=$\frac{\sqrt{3}}{2}$DM,
∴△DMH的周长=DM+DH+MH=DM+$\frac{1}{2}$DM+$\frac{\sqrt{3}}{2}$DM=$\frac{3+\sqrt{3}}{2}$DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,-$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t+$\sqrt{3}$),则D(t,-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$),
∴DM=-$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t+$\sqrt{3}$),则D(t,-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$),
∴DM=-$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t+$\sqrt{3}$-(-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$)=-$\frac{\sqrt{3}}{3}$t2+$\sqrt{3}$t=-$\frac{\sqrt{3}}{3}$(t-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{4}$,
∴当t=$\frac{3}{2}$时,DM有最大值,最大值为$\frac{3\sqrt{3}}{4}$,
此时$\frac{3+\sqrt{3}}{2}$DM=$\frac{3+\sqrt{3}}{2}$×$\frac{3\sqrt{3}}{4}$=$\frac{9\sqrt{3}+9}{8}$,
即△DMH周长的最大值为$\frac{9\sqrt{3}+9}{8}$.
点评 本题为二次函数的综合应用,涉及待定系数法、三角函数的定义、二次函数的性质、方程思想等知识.在(1)中注意函数图象与坐标的交点的求法,在(2)中注意待定系数法的应用,在(3)中找到DH、MH与DM的关系是解题的关键.本题考查知识点较多,综合性较强,难度适中.

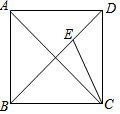 如图,正方形ABCD中,E是BD上一点,BE=BC,则∠BEC的度数是( )
如图,正方形ABCD中,E是BD上一点,BE=BC,则∠BEC的度数是( )| A. | 45° | B. | 60° | C. | 67.5° | D. | 82.5° |
| A. | $\frac{x}{(x-1)^{2}}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{3}{x-1}$ | D. | $\frac{3}{x+1}$ |
 已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )
已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )| A. | 100° | B. | 135° | C. | 155° | D. | 165° |
| A. | a>-4 | B. | a<-4 | C. | a≥-4 | D. | a≤-4 |
| A. | 了解西宁电视台“教育在线”栏目的收视率 | |
| B. | 了解青海湖斑头雁种群数量 | |
| C. | 了解全国快递包裹产生包装垃圾的数量 | |
| D. | 了解某班同学“跳绳”的成绩 |