题目内容
6.若x<0,y>0,化简$\sqrt{{x}^{2}{y}^{3}}$=-xy$\sqrt{y}$.分析 根据二次根式的性质,进行化简,即可解答.
解答 解:$\sqrt{{x}^{2}{y}^{3}}$=(-x)•y$\sqrt{y}$=-xy$\sqrt{y}$,
故答案为:=-xy$\sqrt{y}$.
点评 本题考查二次根式的性质与化简,解决本题的关键是熟记二次根式的性质.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
16.先化简,再求值:$\frac{3x-9}{{x}^{2}-1}$÷$\frac{x-3}{{x}^{2}+2x+1}$-(3-$\frac{3}{1-x}$),其中x=$\sqrt{3}$+1.
18.下列运算正确的是( )
| A. | (x+y2)2=x2+y4 | B. | b6÷b2=b3 | C. | -a2+2a2=a2 | D. | (2y)2×(-y)=-2y3 |
15.我校举行了“建设宜居中山,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
则该班学生成绩的众数和中位数分别是( )
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
16.某公司根据市场计划调整投资策略,对A,B两种产品进行市场调查,收集数据如表:
其中m是待定常数,其值是由生产A的材料的市场价格决定的,变化范围是6≤m≤8,销售B产品时需缴纳$\frac{1}{20}$x2万元的关税,其中x为生产产品的件数,假定所有产品都能在当年售出,设生产A,B两种产品的年利润分别为y1、y2(万元),写出y1、y2与x之间的函数关系式,注明其自变量x的取值范围.
| 项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
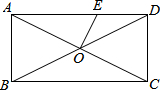 如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5.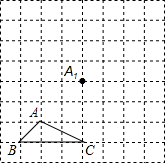 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).