题目内容
12．下列各式与$\sqrt{3}$是同类二次根式的是（ ）| A． | $\sqrt{9}$ | B． | $\sqrt{18}$ | C． | $\sqrt{12}$ | D． | $\sqrt{6}$ |
分析 各项中式子化为最简二次根式，利用同类二次根式定义判断即可．
解答 解：A、原式=3，不符合题意；
B、原式=3$\sqrt{2}$，不符合题意；
C、原式=2$\sqrt{3}$，符合题意；
D、原式=$\sqrt{6}$，不符合题意，
故选C
点评 此题考查了同类二次根式，熟练掌握同类二次根式定义是解本题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
2．在平面直角坐标系中，已知A（-4，1），B（-1，-3），将线段AB向右平移得到线段A′B′，若A′坐标为（-2，1），则点B′在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．下列说法正确的是（ ）
| A． | 直线a、b都经过点m | B． | 直线AB、CD都经过点M | ||
| C． | 延长射线AB到C | D． | 线段、射线、直线中，线段最短 |
20．要使$\sqrt{9+2x}$在实数范围内有意义，则（ ）
| A． | x为任何值 | B． | x≤-$\frac{9}{2}$ | C． | x≥$\frac{9}{2}$ | D． | x≥-$\frac{9}{2}$ |
7．三元一次方程组$\left\{\begin{array}{l}{2x-3y+2z=5}\\{x-2y+3z=-6}\\{3x-y+z=3}\end{array}\right.$ 消去未知数y后，得到的方程组可能是（ ）
| A． | $\left\{\begin{array}{l}{7x+z=4}\\{5x-z=12}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{7x+z=4}\\{x-5z=8}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{7x-z=12}\\{x-5z=28}\\{\;}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{7x-z=4}\\{x-5z=12}\end{array}\right.$ |
4．201718的个位上的数字是（ ）
| A． | 7 | B． | 3 | C． | 9 | D． | 1 |
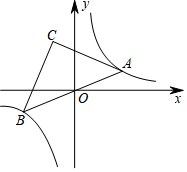如图，点A在双曲线y=$\frac{k}{x}$（k＞0）第一象限分支上，连接AO并延长交另一支于点B，以AB为斜边作等腰直角三角形ABC，已知点C坐标为（-3，7），则k的值为21．
如图，△ABC中，∠C=40°，AD是∠CAB的平分线，BD是△ABC的外角平分线，AD与D交于点D，那么∠D=20°．