题目内容
7.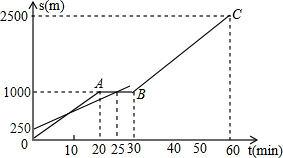 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
分析 (1)根据函数图形得到0≤t≤20、20<t≤30、30<t≤60时,小明所走路程s与时间t的函数关系式;
(2)利用待定系数法求出小明的爸爸所走的路程s与步行时间t的函数关系式,列出二元一次方程组解答即可;
(3)分别计算出小明的爸爸到达公园需要的时间、小明到达公园需要的时间,计算即可.
解答 解:(1)s=$\left\{\begin{array}{l}{50t(0≤t≤20)}\\{1000(20<t≤30)}\\{50t-500(30<t≤60)}\end{array}\right.$;
(2)设小明的爸爸所走的路程s与步行时间t的函数关系式为:s=kt+b,
则$\left\{\begin{array}{l}{25k+b=1000}\\{b=250}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=30}\\{b=250}\end{array}\right.$,
则小明和爸爸所走的路程与步行时间的关系式为:s=30t+250,
当50t-500=30t+250,即t=37.5min时,小明与爸爸第三次相遇;
(3)30t+250=2500,
解得,t=75,
则小明的爸爸到达公园需要75min,
∵小明到达公园需要的时间是60min,
∴小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需减少5min.
点评 本题考查的是一次函数的应用,掌握待定系数法求一次函数解析式、读懂函数图象是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
16.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为( )
| A. | x1=-3,x2=-1 | B. | x1=1,x2=3 | C. | x1=-1,x2=3 | D. | x1=-3,x2=1 |
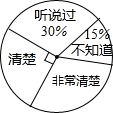 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.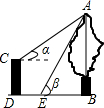 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)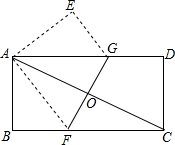 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.