题目内容
18.任取不等式组$\left\{\begin{array}{l}{k-3≤0}\\{2k+5>0}\end{array}\right.$的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的概率为$\frac{1}{3}$.分析 首先求得不等式组$\left\{\begin{array}{l}{k-3≤0}\\{2k+5>0}\end{array}\right.$的一个整数解,关于x的方程:2x+k=-1的解为非负数时,k的整数解,继而求得答案.
解答 解:∵解不等式组$\left\{\begin{array}{l}{k-3≤0}\\{2k+5>0}\end{array}\right.$的解集为:-$\frac{5}{2}$<k≤3,
∴整数解为:-2,-1,0,1,2,3,
关于x的方程:2x+k=-1的解为:x=-$\frac{k+1}{2}$,
∵关于x的方程:2x+k=-1的解为非负数,
∴k+1≤0,
解得:k≤-1,
∴能使关于x的方程:2x+k=-1的解为非负数的为:-1,-2;
∴能使关于x的方程:2x+k=-1的解为非负数的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式的应用、不等式组的整数解以及一元一次方程的解.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.如图,是由若干个大小相同的正方体搭成的几何体的三视图,该几何体所用的正方体的个数是( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
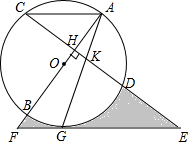 如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.
如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )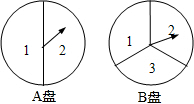 小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.
小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.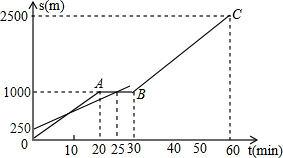 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.