题目内容
16.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为( )| A. | x1=-3,x2=-1 | B. | x1=1,x2=3 | C. | x1=-1,x2=3 | D. | x1=-3,x2=1 |
分析 直接利用抛物线与x轴交点求法以及结合二次函数对称性得出答案.
解答 解:∵二次函数y=ax2-2ax+c的图象经过点(-1,0),
∴方程ax2-2ax+c=0一定有一个解为:x=-1,
∵抛物线的对称轴为:直线x=1,
∴二次函数y=ax2-2ax+c的图象与x轴的另一个交点为:(3,0),
∴方程ax2-2ax+c=0的解为:x1=-1,x2=3.
故选:C.
点评 此题主要考查了抛物线与x轴的交点,正确应用二次函数对称性是解题关键.

练习册系列答案
相关题目
8.如图,是由若干个大小相同的正方体搭成的几何体的三视图,该几何体所用的正方体的个数是( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
5.姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:在每一个象限内,y值随x值的增大而减小.根据他们的描述,姜老师给出的这个函数表达式可能是( )
| A. | y=3x | B. | $y=\frac{3}{x}$ | C. | $y=-\frac{1}{x}$ | D. | y=x2 |
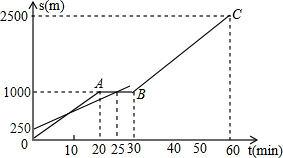 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.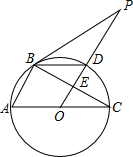 如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD. 如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )
如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( ) 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的图象可能是( )
二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的图象可能是( )


