题目内容
19.已知|x-y+2|+$\sqrt{x+y-2}$=0,则x2-y2的值为-4.分析 由|x-y+2|+$\sqrt{x+y-2}$=0,根据非负数的性质,可求得x-y与x+y的值,继而由x2-y2=(x-y)(x+y)求得答案.
解答 解:∵|x-y+2|+$\sqrt{x+y-2}$=0,
∴x-y+2=0,x+y-2=0,
∴x-y=-2,x+y=2,
∴x2-y2=(x-y)(x+y)=-4.
故答案为:-4.
点评 此题考查了平方差公式分解因式以及非负数的性质.注意根据非负数的性质求得x-y与x+y的值是关键.

练习册系列答案
相关题目
14.下列实数中,有理数是( )
| A. | $\sqrt{8}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101001001 |
8.如图,是由若干个大小相同的正方体搭成的几何体的三视图,该几何体所用的正方体的个数是( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
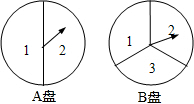 小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.
小明和小亮用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则小明胜,否则小亮胜.这个游戏对双方公平吗?请说明理由.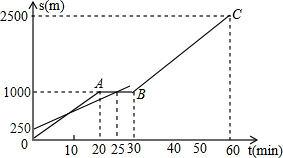 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.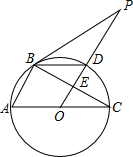 如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD. 如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )
如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )