题目内容
10.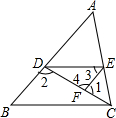 如图,已知∠1+∠2=180°,∠3=∠B,
如图,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠ACB,请补充完成下面证明过程.
证明:∵∠1+∠2=180°(已知)
∠1+∠4=180°邻补角的定义
∴∠2=∠4(同角的补角相等)
∴AB∥EF内错角相等,两直线平行
∴∠3=∠AOE(两直线平行,内错角相等)
∵∠3=∠B已知
∴∠B=∠ADE等量代换
∴DE∥BC(同位角相等,两直线平行)
∴∠AED=∠ACB两直线平行,同位角相等.
分析 由条件可先证明EF∥AB,再利用平行线的性质可得到∠3=∠ADE=∠B,可证明DE∥BC,可证得∠AED=∠ACB,据此填空即可.
解答 证明:∵∠1+∠2=180°(已知),
∠1+∠4=80° 邻补角的定义,
∴∠2=∠4(同角的补角相等),
∴AB∥EF 内错角相等,两直线平行,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B 已知,
∴∠B=∠ADE 等量代换,
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB 两直线平行,同位角相等.
故答案为:邻补角的定义;∠4;内错角相等,两直线平行;∠AOE;已知;等量代换;BC;两直线平行,同位角相等.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
20.30等于( )
| A. | 3 | B. | 0 | C. | 1 | D. | -1 |
1.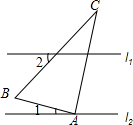 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
18.在平面直角坐标系中,点P(3,-x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下列说法中,错误的是( )
| A. | $\sqrt{2}$是2的一个平方根 | B. | -$\sqrt{2}$的平方是2 | ||
| C. | 2的平方根就是2的算术平方根 | D. | $\sqrt{2}$是2的算术平方根 |
15.在下列各对数值中,是方程2x+3y=-6的解的一组数值是( )
| A. | $\left\{\begin{array}{l}x=0\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=-3\\ y=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$ |
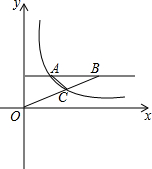 如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.
如图,反比例函数y=$\frac{6}{x}$(x>0)上任取一点A,过A作AB∥x轴,OB交图象于C,OC:BC=2:3,求△ABC面积.