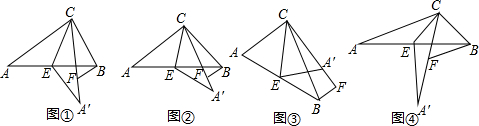
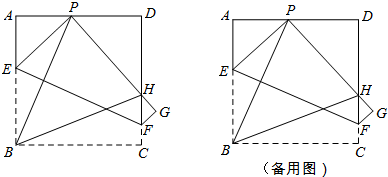
��Ŀ����
16���о�����ij�����Ͳ�Ʒ�IJ�������������о���ΪͶ�����ڼס����������������۸ò�Ʒ�ṩ�����³ɹ�����һ��������Ϊx���֣�ʱ�������ȫ������y����Ԫ����x�����ϵʽy=$\frac{1}{10}$x2+5x+90��Ͷ���г�������ȫ���۳������ڼס�������ÿ�ֵ��ۼ�p����p������Ԫ������x����һ�κ�����ϵ����ע��������=�����۶�-ȫ�����ã�
��1���ɹ��������ڼ�����������x��ʱ��p��=-$\frac{1}{20}$x+14�������ú�x�Ĵ���ʽ��ʾ�ص���������۶����������W������Ԫ����x֮��ĺ�����ϵʽ��
��2���ɹ����������ҵ�����������x��ʱ��p��=-$\frac{1}{10}$x+n��nΪ�������������ҵص�������������Ϊ35��Ԫ����ȷ��n��ֵ��
��3�����ʽ����������ȶ������ص�Ӱ�죬ijͶ���̼ƻ���һ�����������۸ò�Ʒ18�֣����ݣ�1������2���еĽ��������ͨ������������ߣ�ѡ���ڼػ����ҵز������ܻ������������
���� ��1������������=�����۶�-ȫ�����ü����������W������Ԫ����x֮��ĺ�����ϵʽ��
��2���������W������Ԫ����x֮��ĺ�����ϵʽ���������������Ϊ35��Ԫ�����n��ֵ��
��3���ֱ����x=18ʱ��W����W����ֵ��ͨ���Ƚ�W����W����С�Ϳ�����Ͷ��������ѡ��
��� �⣺��1���ص���������۶�Ϊ��-$\frac{1}{20}$x+14��•x=��-$\frac{1}{20}$x2+14x����Ԫ��
w��=��-$\frac{1}{20}$x2+14x��-��$\frac{1}{10}$x2+5x+90��=-$\frac{3}{20}$x2+9x-90��
��2�����ҵ�������������ʱ��
������
w��=-$\frac{1}{10}$x2+nx-��$\frac{1}{10}$x2+5x+90��
=-$\frac{1}{5}$x2+��n-5��x-90��
��$\frac{4ac-{b}^{2}}{4a}$=$\frac{4����-\frac{1}{5}������-90��-��n-5��^{2}}{4����-\frac{1}{5}��}$=35��
���n=15��-5��
�����飬n=-5�������⣬��ȥ��
��n=15��
��3�����ҵ�������������ʱ��������
w��=-$\frac{1}{5}$x2+10x-90��
��x=18������ʽ����w��=25.2����Ԫ����
��x=18����w��=-$\frac{3}{20}$x2+9x-90��
��w��=23.4����Ԫ����
��W����W����
��Ӧѡ�ҵأ�
���� ������һ����ѷ���ѡ���⣬ͨ�����㡢�Ƚ�ͬһ���Ա�������������ֵ�Ĵ�С��ѡ����ѷ���������������=�����۶�-ȫ�����ü����������W������Ԫ����x֮��ĺ�����ϵʽ������W������Ԫ����x֮��ĺ�����ϵʽ���ֱ����x=18ʱ��W����W����ֵ��ͨ���Ƚ�W����W����С�Ϳ�����Ͷ��������ѡ��

 Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ�Ʊ���ͳ��ͼ��ͼ����Ϣ������������֪A��B��������ı�Ϊ1��5��
Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ�Ʊ���ͳ��ͼ��ͼ����Ϣ������������֪A��B��������ı�Ϊ1��5��| ��� | ���x��Ԫ | ���� |
| A | 1��x��50 | a |
| B | 50��x��100 | 10 |
| C | 100��x��150 | |
| D | 150��x��200 | |
| E | x��200 |
��1��a=2�������������������50��
��2����ȫ����������ͳ�Ʊ��;���ͳ��ͼ1����
��3������������1500��ס���������������Ϣ���ƣ�ȫ����������150Ԫ�Ļ����Ƕ��٣�
| A�� | $\frac{0.1x-0.3y}{0.2x+y}$=$\frac{x-3y}{2x+y}$ | B�� | $\frac{x+y}{x-y}$=0 | ||
| C�� | $\frac{-x+y}{x-y}$=-1 | D�� | $\frac{b}{a}$=$\frac{{b}^{2}}{{a}^{2}}$ |

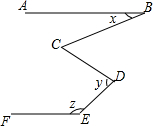 ��ͼ����֪AB��EF����C=45�㣬д��x��y��z�Ĺ�ϵʽx+y+z=225�㣮
��ͼ����֪AB��EF����C=45�㣬д��x��y��z�Ĺ�ϵʽx+y+z=225�㣮