题目内容
8.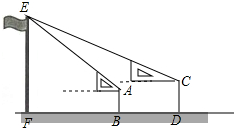 如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)
如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)
分析 过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.1m.由小明站在B点测得旗杆顶端E点的仰角为45°,可得△AEM是等腰直角三角形,继而得出得出AM=ME,设AM=ME=xm,则CN=(x+6)m,EN=(x-0.1)m.在Rt△CEN中,由tan∠ECN=$\frac{EN}{CN}$=$\frac{\sqrt{3}}{3}$,代入CN、EN解方程求出x的值,继而可求得旗的高度.
解答 解:过点A作AM⊥EF于M,过点C作CN⊥EF于N,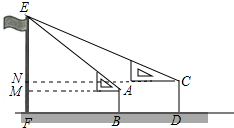
∴MN=0.1m,
∵∠EAM=45°,
∴AM=ME,
设AM=ME=xm,
则CN=(x+6)m,EN=(x-0.1)m,
∵∠ECN=30°,
∴tan∠ECN=$\frac{EN}{CN}$=$\frac{x-0.1}{x+6}$=$\frac{\sqrt{3}}{3}$,
解得:x≈8.41,
则EF=EM+MF≈8.41+1.6=10.0(m).
答:旗杆的高EF为10.0m
点评 本题考查了解直角三角形的问题.该题是一个比较常规的解直角三角形问题,建立模型比较简单,但求解过程中涉及到根式和小数,算起来麻烦一些.

练习册系列答案
相关题目
19.下列四个图形中,轴对称图形有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.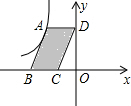 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
13.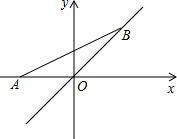 如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | D. | (-$\frac{1}{2}$,-$\frac{1}{2}$) |
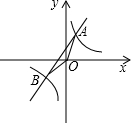 如图,是一次函数与反比例函数的图象.已知A(1,2),B点的横坐标为-2.
如图,是一次函数与反比例函数的图象.已知A(1,2),B点的横坐标为-2. 已知;如图,E,F是?ABCD的对角线AC上的两点,且AF=EC,请判断DE和BF是否相等,你有几种方法说明理由?
已知;如图,E,F是?ABCD的对角线AC上的两点,且AF=EC,请判断DE和BF是否相等,你有几种方法说明理由?