题目内容
3.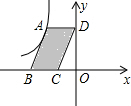 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
分析 作AE⊥BC于E,由四边形ABCD为平行四边形得AD∥x轴,则可判断四边形ADOE为矩形,所以S平行四边形ABCD=S矩形ADOE,根据反比例函数k的几何意义得到S矩形ADOE=|-k|,利用反比例函数图象得到.
解答 解: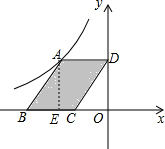 作AE⊥BC于E,如图,
作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD∥x轴,
∴四边形ADOE为矩形,
∴S平行四边形ABCD=S矩形ADOE,
而S矩形ADOE=|-k|,
∴|-k|=6,
而k<0,即k<0,
∴k=-6.
故选B.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13.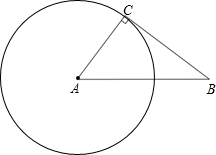 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
18.计算(-8)×3÷(-2)2得( )
| A. | -6 | B. | 6 | C. | -12 | D. | 12 |
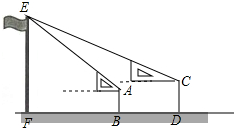 如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)
如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1) 如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.
如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.