题目内容
18.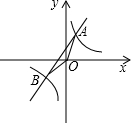 如图,是一次函数与反比例函数的图象.已知A(1,2),B点的横坐标为-2.
如图,是一次函数与反比例函数的图象.已知A(1,2),B点的横坐标为-2.(1)求反比例函数的表达式;
(2)求一次函数的表达式;
(3)试求S△AOB.
分析 (1)设出反比例函数的解析式,将点A代入利用待定系数法即可得出反比例函数的解析式;
(2)将点B的横坐标代入反比例函数的解析式,求得B点的坐标,设出一次函数的解析式,再将点A,B代入,列出关于k和b的方程组,从而得出答案;
(3)设直线交y轴于C,则OC=1,然后根据S△AOB=S△BOC+S△AOC求得即可.
解答 解:(1)设反比例函数的解析式分别为:y=$\frac{a}{x}$,把点A代入,得2=$\frac{a}{1}$,解得a=2,
∴反比例函数的解析式为:y=$\frac{2}{x}$;
(2)把x=-2代入y=$\frac{2}{x}$,得y=-1,
∴B(-2,-1),
设一次函数的解析式分别为:y=kx+b,
把点A,B代入y=kx+b,得$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
故一次函数的解析式为y=x+1.
(3)设直线交y轴于C,则OC=1,
∴S△AOB=S△BOC+S△AOC=$\frac{1}{2}$×OC×2+$\frac{1}{2}$×OC×1=$\frac{3}{2}$.
点评 本题考查了反比例函数和一次函数的交点问题,反比例函数和一次函数分别知道图象上的一点和两点即可得出它的解析式;也考查了三角形的面积.

练习册系列答案
相关题目
17.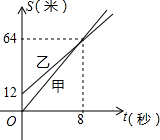 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
13.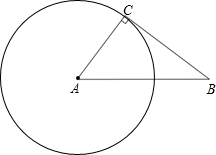 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
3.若∠α与∠β是内错角,且∠α=50°时,则∠β的度数为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 无法确定 |
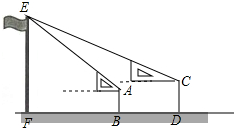 如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)
如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)