题目内容
20. 已知;如图,E,F是?ABCD的对角线AC上的两点,且AF=EC,请判断DE和BF是否相等,你有几种方法说明理由?
已知;如图,E,F是?ABCD的对角线AC上的两点,且AF=EC,请判断DE和BF是否相等,你有几种方法说明理由?
分析 方法一:根据平行四边形的对边相等可得AB=CD,对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠BAF=∠DCE,然后利用“边角边”证明△ABF和△CDE全等,根据全等三角形对应边相等可得DE=BF;
方法二:连接BE、BD、DF,根据平行四边形对角线互相平分可得OA=OC,OB=OD,再求出OE=OF,然后判断出四边形BFDE是平行四边形,然后根据平行四边形对边相等证明即可.
解答 解:DE=BF.
方法一:在?ABCD中,AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF和△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{∠BAF=∠DCE}\\{AF=EC}\end{array}\right.$,
∴△ABF≌△CDE(SAS),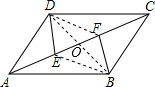
∴DE=BF;
方法二:如图,连接BE、BD、DF,
在?ABCD中,OA=OC,OB=OD,
∵AF=EC,
∴EC-OC=AF-OA,
即OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形,
∴DE=BF.
点评 本题考查了平行四边形的性质,全等三角形的判定与性质,理解平行四边形的对边平行且相等,是解答本题的关键.

练习册系列答案
相关题目
5.小敏为了解本市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
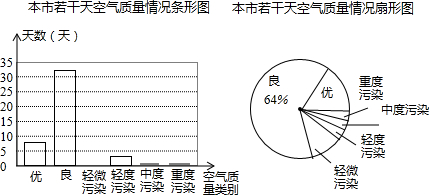
根据以上信息,如下结论错误的是( )

根据以上信息,如下结论错误的是( )
| A. | 被抽取的天数为50天 | |
| B. | 空气轻微污染的所占比例为10% | |
| C. | 扇形统计图中表示优的扇形的圆心角度数57.6° | |
| D. | 估计该市这一年(365天)达到优和良的总天数不多于290天 |
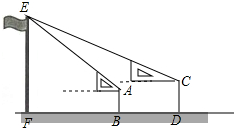 如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1)
如图,某校九年级某班开展数学活动,小明和小军合作一副三角板测量学校旗杆的高度,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,F、B、D三点在一条直线上,已知小明和小军相距(BD)6米,小明的身高(AB)1.6米,小军的身高(CD)1.7米,求旗杆的高EF的长(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1) 如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.
如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.