题目内容
11.已知有理数a、b满足a+b>0,且|a|=2,|b|=3,求|a-$\frac{1}{3}$|-(b-1)的值.分析 首先根据a+b>0,且|a|=2,|b|=3,可得a=2,b=3或a=-2,b=3;然后分类讨论,求出算式|a-$\frac{1}{3}$|-(b-1)的值是多少即可.
解答 解:∵|a|=2,|b|=3,
∴a=2或-2,b=3或-3,
又∵a+b>0,
∴a=2,b=3或a=-2,b=3.
①a=2,b=3时,
|a-$\frac{1}{3}$|-(b-1)
=|2-$\frac{1}{3}$|-(3-1)
=$\frac{5}{3}-2$
=$-\frac{1}{3}$
②a=-2,b=3时,
|a-$\frac{1}{3}$|-(b-1)
=|-2-$\frac{1}{3}$|-(3-1)
=$\frac{7}{3}-2$
=$\frac{1}{3}$
点评 (1)此题主要考查了代数式求值问题,要熟练掌握,解答此题的关键是要明确:如果给出的代数式可以化简,要先化简再求值.
(2)此题还考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
1.观察下列算式中的规律,你认为220的末位数字是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
3.下列各组数中,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 3k,4k,5k(k>0) | C. | 6,8,11 | D. | 5,12,23 |
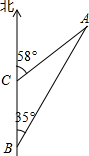 如图,海中有一小岛,它周围8海里内有暗礁,渔船跟踪渔群由南向北航行,在B点测得小岛A在北偏东35°方向,航行12海里到达C点,测得小岛A在北偏东58°方向.如果渔船不改变航向,继续向北航行,有没有触礁的危险?(tan35°≈0.7002,tan581°≈1.6003,精确到0.1海里)
如图,海中有一小岛,它周围8海里内有暗礁,渔船跟踪渔群由南向北航行,在B点测得小岛A在北偏东35°方向,航行12海里到达C点,测得小岛A在北偏东58°方向.如果渔船不改变航向,继续向北航行,有没有触礁的危险?(tan35°≈0.7002,tan581°≈1.6003,精确到0.1海里)