题目内容
3.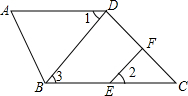 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.
分析 首先证明直线AD∥BC,进而得到∠1=∠3,结合∠1=∠2即可得到∠2=∠3,即可判定BD∥FE,于是结论得证.
解答 解:∵∠ABC=180°-∠A,
∴∠ABC+∠A=180°,
∴AD∥BC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴BD∥EF.
∵BD⊥CD,
∴EF⊥CD.
点评 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.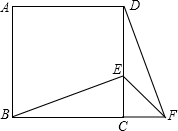 如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
 如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
如图,在正方形ABCD中,E位DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )| A. | 15° | B. | 10° | C. | 20° | D. | 25° |
16.关于x的分式方程$\frac{m-1}{x-1}$=2的解为正数,则m的取值范围是( )
| A. | m>-1 | B. | m≠1 | C. | m>1 | D. | m>-1且m≠1 |
8.若2x=5y,则下列式子中错误的是( )
| A. | $\frac{y}{x}$=$\frac{5}{2}$ | B. | $\frac{y}{x}$=$\frac{2}{5}$ | C. | $\frac{x+y}{x}$=$\frac{7}{5}$ | D. | $\frac{x-y}{y}$=$\frac{3}{2}$ |

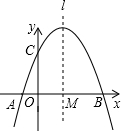 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.