题目内容
13.计算:$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+6xy+5{y}^{2}}$•$\frac{x+5y}{{x}^{2}-2x-{y}^{2}+2y}$.分析 先将分式的分子与分母进行因式分解
解答 解:原式=$\frac{(x-y)(x+y)}{(x+y)(x+5y)}$•$\frac{x+5y}{(x-y)(x+y)-2(x-y)}$
=$\frac{(x-y)(x+y)}{(x+y)(x+5y)}$•$\frac{x+5y}{(x-y)(x+y-2)}$
=$\frac{1}{x+y-2}$
点评 本题考查分式的乘除法,涉及因式分解法,题目较为综合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.设A=x2+1,B=-2x+x2,则2B-3A可化简为( )
| A. | 4x2+1 | B. | -x2-4x-3 | C. | x2-4x-3 | D. | x2-3 |
1.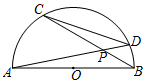 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )| A. | 16:9 | B. | 3:4 | C. | 4:3 | D. | 9:16 |
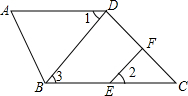 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF交CD于F,若∠1=∠2,求证:EF⊥CD.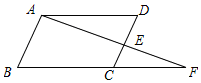 根据解答过程填空(写出推理理由或根据):
根据解答过程填空(写出推理理由或根据):