题目内容
 如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为
如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为考点:等腰梯形的性质
专题:
分析:根据角平分线的定义可得∠ABD=∠CBD,根据两直线平行,内错角相等可得∠CBD=∠ADB,从而得到∠ABD=∠ADB,根据等角对等边可得AB=AD,再求出∠BDC=90°,∠CBD=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出BC=2CD,然后根据梯形的周长列出方程求解即可.
解答:解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠CBD=∠ADB,
∴∠ABD=∠ADB,
∴AB=AD,
∵∠A=120°,
∴∠ABD=∠ADB=
×(180°-120°)=30°,
在等腰梯形ABCD中,∠ADC=∠A=120°,
∴∠BDC=120°-30°=90°,
又∵∠CBD=∠ADB=30°,
∴BC=2CD,
∴梯形的周长=AB+BC+CD+AD=AD+2AD+AD+AD=5AD,
∵梯形的周长为10,
∴5AD=10,
解得AD=2.
故答案为:2.
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠CBD=∠ADB,
∴∠ABD=∠ADB,
∴AB=AD,
∵∠A=120°,
∴∠ABD=∠ADB=
| 1 |
| 2 |
在等腰梯形ABCD中,∠ADC=∠A=120°,
∴∠BDC=120°-30°=90°,
又∵∠CBD=∠ADB=30°,
∴BC=2CD,
∴梯形的周长=AB+BC+CD+AD=AD+2AD+AD+AD=5AD,
∵梯形的周长为10,
∴5AD=10,
解得AD=2.
故答案为:2.
点评:本题考查了等腰梯形的性质,平行线的性质,等角对等边,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并求出梯形的各边与AD的关系是解题的关键.

练习册系列答案
相关题目
若a=-4b,则对a的任何值多项式a2+3ab-4b2+2的值( )
| A、总是2 | B、总是0 |
| C、总是1 | D、是不确定的值 |
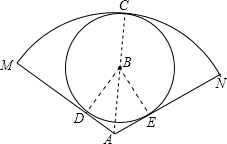 如图,∠MAN=120°,⊙B的半径为r,⊙B与
如图,∠MAN=120°,⊙B的半径为r,⊙B与
 已知抛物线y=ax2+bx+c,顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).
已知抛物线y=ax2+bx+c,顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).