题目内容
5.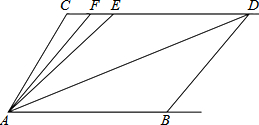 如图,已知CD∥AB,∠C=∠B=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
如图,已知CD∥AB,∠C=∠B=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.(1)说明:AC∥BD;
(2)说明:AD平分∠EAB;
(3)求∠FAD的度数.
分析 (1)根据平行线的性质得到∠C+∠CAB=180°,等量代换得到∠CAB+∠B=180°,根据平行线的判定定理即可得到结论;
(2)根据平行线的性质得到∠ADE=∠BAD,等量代换得到∠EAD=∠BAD,即可得到结论;
(3)先根据平行线的性质求出∠CAB的度数,∠BAD=∠EAD,再由∠EAD=∠EDA,AF平分∠CAE可得出∠FAD=$\frac{1}{2}$∠CAB,由此可得出结论;
解答 解:(1)∵CD∥AB,
∴∠C+∠CAB=180°,
∵∠C=∠B,
∴∠CAB+∠B=180°,
∴AC∥BD;
(2)∵AB∥CD,
∴∠ADE=∠BAD,
∵∠EAD=∠EDA,
∴∠EAD=∠BAD,
∴AD平分∠EAB;
(3)∵CD∥AB,∠C=110°,
∴∠CAB=70°,∠BAD=∠EAD,
∵∠EAD=∠EDA,
∴∠EAD=∠BAD=$\frac{1}{2}$∠EAB.
∵AF平分∠CAE,
∴∠FAD=∠FAE+∠EAD=$\frac{1}{2}$∠CAB=$\frac{1}{2}$×70°=35°.
点评 本题考查的是平行线的性质和判定,三角形外角的性质,角平分线的定义,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
13. 将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
 将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
9.下列说法正确的是( )
| A. | 方程的解等于零,就是增根 | |
| B. | 使最简公分母的值为零的解是增根 | |
| C. | 使分子的值为零的解是增根 | |
| D. | 只有使所有分母的值为零的解才是增根 |
7.下列各式中无意义的是( )
| A. | $\root{3}{-2}$ | B. | $\root{3}{a}$ | C. | $\sqrt{-3}$ | D. | $\sqrt{{a}^{2}}$ |
 如图,三角形ABC在平面直角坐标系中,
如图,三角形ABC在平面直角坐标系中, 已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
已知直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).