题目内容
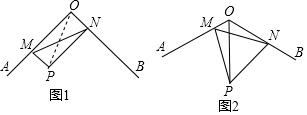
13. 如图,在四边形ABCD中,DC∥AB,BD平分∠ABC,∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
如图,在四边形ABCD中,DC∥AB,BD平分∠ABC,∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.
分析 △DEF为等边三角形.欲证明△DEF为等边三角形,只需推知△DEF为等腰三角形,且有一内角为60度即可.
解答 证明:∵BD平分∠ABC,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=30°.
∵DC∥AB
∴∠CDB=∠ABD=30°.
∴∠CDB=∠CBD=30°,
∴CD=CB.
∵CF⊥BD.
∴DF=BF,
∵DE⊥AB,
∴EF为Rt△BDE斜边BD上的中线,
∴DF=BF=EF,
∵∠DBE=30°.
∴∠BDE=60°,
∴△DEF为等边三角形.
点评 本题考查了梯形的性质及等腰三角形的判定及判定,包括了等边三角形的判定及性质,题目难度适中.

练习册系列答案
相关题目
4.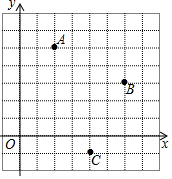 如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
 如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )| A. | (0,0) | B. | (0,1) | C. | (3,2) | D. | (1,0) |
3.实数a,b,c满足a<b<0<c,则下列式子中正确的是( )
| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b<c | D. | -a-c>-b-c |