题目内容
11.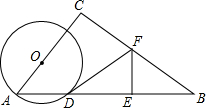 如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.(1)求证:DF为⊙O的切线;
(2)若AO=x,DF=y,求y与x之间的函数关系式.
分析 (1)连接OD,由于EF是BD的中垂线,DF=BF.从而可知∠FDB=∠B,又因为OA=OD,所以∠OAD=∠ODA,从而可证明∠ODF=90°;
(2)连接OF,由题意可知:AO=x,DF=y,OC=6-x,CF=8-y,然后在Rt△COF中与Rt△ODF中利用勾股定理分别求出OF,化简原式即可求出答案.
解答 (1)连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵EF是BD的中垂线,
∴DF=BF.
∴∠FDB=∠B,
∵∠C=90°,
∴∠OAD+∠B=90°.
∴∠ODA+∠FDB=90°.
∴∠ODF=90°,
又∵OD为⊙O的半径,
∴DF为⊙O的切线,
(2)连接OF.
在Rt△ABC中,
∵∠C=90°,sinA=$\frac{4}{5}$,AB=10,
∴AC=6,BC=8,
∵AO=x,DF=y,
∴OC=6-x,CF=8-y,
在Rt△COF中,
OF2=(6-x)2+(8-x)2
在Rt△ODF中,
OF2=x2+y2
∴(6-x)2+(8-x)2=x2+y2,
∴y=-$\frac{3}{4}$x+$\frac{25}{4}$(0<x≤6)
点评 本题考查圆的综合问题,涉及切线的性质,勾股定理、垂直平分线的性质等知识,综合程度较高.

练习册系列答案
相关题目
19.已知∠A和∠B互余,∠A比∠B大10°,设∠A、∠B的度数分别为x°、y°,下列方程组在符合题意的是( )
| A. | $\left\{\begin{array}{l}{x+y=90}\\{x=y+10}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=90}\\{x=y-10}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=180}\\{x=y-10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{x=y+10}\end{array}\right.$ |
6.下面各数中,比-1大的数是( )
| A. | -5 | B. | -$\frac{3}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
16.正三角形内切圆的半径为$\sqrt{3}$,则此正三角形的边长是( )
| A. | 2$\sqrt{3}$ | B. | 6 | C. | 3 | D. | 2 |
3.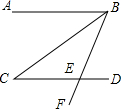 如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
1.将直线y=$\frac{1}{2}$x+1向右平移4个单位后得到直线y=kx+b,则k+b的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
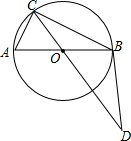 如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.
如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.