题目内容
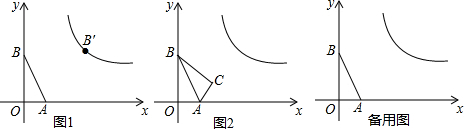
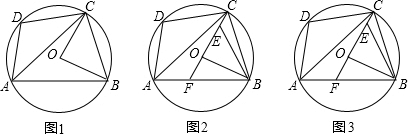
1.已知:如图1,在平面直角坐标系中,点A(1,0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′恰在反比例函数y=$\frac{k}{x}$(x>0)的图象上.(1)求k的值;
(2)如图2,将△AOB(点O为坐标原点)沿AB翻折得到△ACB,求同一平面内点C的坐标;
(3)在同一平面内,是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF(即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=$\frac{k}{x}$ (x>0)的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)利用平移规律确定出B′的坐标,代入反比例解析式求出k的值即可;
(2)利用待定系数法求出直线AB解析式,利用对称性质确定出直线OC解析式,联立直线AB与直线OC解析式求出线段OC中点坐标,设出C坐标,求出b的值,即可确定出C坐标;
(3)△AOB放大为原来的两倍后得到△DEF,且△DEF∽△AOB,则点D和F一定在反比例函数图象上,设出P与D坐标,根据该相似三角形的对应边成比例列出比例式并解答.
解答 解:(1)点B沿x轴正方向平移3个单位长度得到对应点B′的坐标是(3,2),
代入y=$\frac{k}{x}$得:k=6;
(2)设直线AB的解析式是y=mx+n,则$\left\{\begin{array}{l}{n=2}\\{m+n=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=2}\end{array}\right.$,
∴直线AB的解析式是y=-2x+2,
∴OC的解析式是y=$\frac{1}{2}$x.
解方程组$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{1}{2}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=\frac{2}{5}}\end{array}\right.$,
设C的坐标是(b,$\frac{1}{2}$b),
可得:$\frac{1}{2}$b=$\frac{4}{5}$,
解得:b=$\frac{8}{5}$.
则C的坐标是($\frac{8}{5}$,$\frac{4}{5}$);
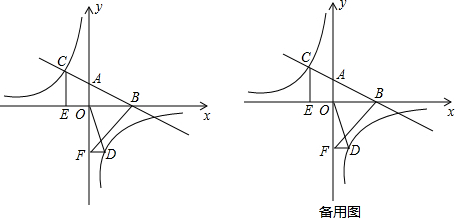
(3)如图3中,△AOB放大为原来的两倍后得到△DEF,且△DEF∽△AOB,D和F在反比例函数图象上,设D(m,$\frac{6}{m}$)则易知F(m+2,$\frac{6}{m}$-4),
∴(m+2)($\frac{6}{m}$-4)=6,
解得m=1或-3(舍弃),
∴D(1,6),F(3,2),
∴直线BD的解析式为y=4x+2
直线AF的解析式为y=x-1,
由$\left\{\begin{array}{l}{y=4x+2}\\{y=x-1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴P(-1,-2),
连接BF、AD,BF交AD于P′,易知P′(1,2),
∴P′(1,2)或P(-1,-2)即为位似中心,(图只是作为参考!)
综上所述,P坐标为(-1,-2)或(1,2).
点评 本题考查了反比例函数综合题.解题时,利用了待定系数法求一次函数、反比例函数的解析式,反比例函数图象上点的坐标特征以及位似图形的性质.要注意(3)中x的取值范围.该题难度比较大.

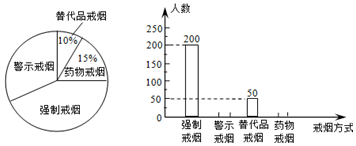
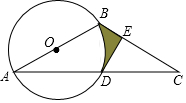 如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.
如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.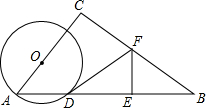 如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.