题目内容
16.正三角形内切圆的半径为$\sqrt{3}$,则此正三角形的边长是( )| A. | 2$\sqrt{3}$ | B. | 6 | C. | 3 | D. | 2 |
分析 已知内切圆半径,可过内心向正三角形的一边作垂线,连接顶点与内切圆心,构造直角三角形求解.
解答 解:过O点作OD⊥AB,则OD=$\sqrt{3}$.
∵O是△ABC的内心,
∴∠OAD=30°;
Rt△OAD中,∠OAD=30°,OD=$\sqrt{3}$,
∴AD=$\frac{OD}{tan30°}$=3,
∴AB=2AD=6.
故选:B.
点评 本题主要考查等边三角形的性质、三角形内切圆的性质,关键在于作辅助线构建直角三角形.

练习册系列答案
相关题目
7.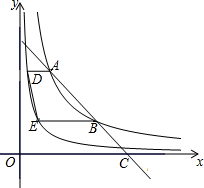 如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )
如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )
 如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )
如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | $\frac{11}{2}$ |
4.不等式1-2x>1的解集为( )
| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
1.化简(x3)2的结果是( )
| A. | 2x3 | B. | x5 | C. | x6 | D. | x9 |
8.下列运算正确的是( )
| A. | a2•a4=a6 | B. | (a2)4=a4 | C. | 3(a-b)=3a-b | D. | a-b2=a2-ab+b2 |
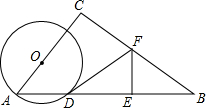 如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
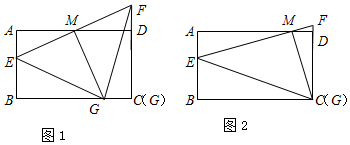
如图,在Rt△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.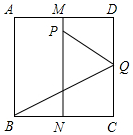 如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.
如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.