题目内容
12.先化简,再求值:(x-y+$\frac{4xy}{x-y}$)(x+y-$\frac{4xy}{x+y}$),其中x和y是方程3x+2y=8的正整数解.分析 先根据分式混合运算的法则把原式进行化简,再根据x和y是方程3x+2y=8的正整数解求出x、y的值,代入原式进行计算即可.
解答 解:原式=$\frac{(x+y)^{2}}{x-y}$•$\frac{(x-y)^{2}}{x+y}$
=$\frac{{(x+y)}^{2}}{x-y}$•$\frac{x+y}{(x-y)^{2}}$
=$\frac{(x+{y)}^{3}}{{(x-y)}^{3}}$,
∵x和y是方程3x+2y=8的正整数解,
∴当x=1时,y=$\frac{5}{2}$(舍去);
当x=2时,y=1;
∴当x=2,y=1时,原式=$\frac{{(2+1)}^{3}}{{(2-1)}^{3}}$=27.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
19.若关于x的一元二次方程kx2-4x+3=0有实数根,则k的非负整数值是( )
| A. | 1 | B. | 0,1 | C. | 1,2 | D. | 1,2,3 |
17.下列各式中,计算结果为x2-16y2的是( )
| A. | (x+2y)(x-8y) | B. | (x+y)(x-16y) | C. | (-4y+x)(4y+x) | D. | (-x-4y)(x+4y) |
2.若关于x的分式方程$\frac{x-6}{x-5}+1=\frac{k}{5-x}$有增根,则k的值是( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
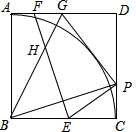 点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)
点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)