题目内容
已知函数y=(k-3)x2+2x+1的图象与x轴有公共点,则k的取值范围是 .
考点:抛物线与x轴的交点
专题:
分析:利用二次函数图象与x轴交点个数与b2-4ac的关系,以及一次函数与x轴必有一个交点进而得出答案.
解答:解:∵函数y=(k-3)x2+2x+1的图象与x轴有公共点,
∴当k-3≠0,则b2-4ac≥0,
即4-4(k-3)×1=16-4k≥0,
解得:k≤4,且k≠3;
当k-3=0,则函数y=(k-3)x2+2x+1=2x+1,此函数一定与x轴有一个交点,
综上所述:k≤4,且k≠3或k=3.
故答案为:k≤4,且k≠3或k=3.
∴当k-3≠0,则b2-4ac≥0,
即4-4(k-3)×1=16-4k≥0,
解得:k≤4,且k≠3;
当k-3=0,则函数y=(k-3)x2+2x+1=2x+1,此函数一定与x轴有一个交点,
综上所述:k≤4,且k≠3或k=3.
故答案为:k≤4,且k≠3或k=3.
点评:此题主要考查了抛物线与x轴的交点,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
边长为2的正方形的面积是4,边长为3的正方形的面积是9,则面积是6的正方形的边长a满足( )
| A、a是整数 |
| B、2<a<3 |
| C、2<a<3,且a为分数 |
| D、a不存在 |
 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.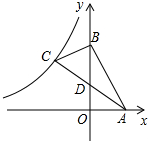 如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且
如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且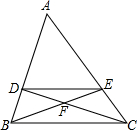 如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=
如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=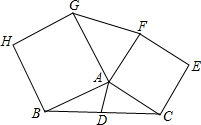 如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证:
如图,已知AD是△ABC的中线,分别以AB、AC为边向外作正方形,得正方形ABHG和正方形ACEF,求证: 如图,在⊙O中,点A、O、D和点B、O、C分别在一条直线上,图中共有
如图,在⊙O中,点A、O、D和点B、O、C分别在一条直线上,图中共有