题目内容
边长为2的正方形的面积是4，边长为3的正方形的面积是9，则面积是6的正方形的边长a满足（ ）
| A、a是整数 |
| B、2＜a＜3 |
| C、2＜a＜3，且a为分数 |
| D、a不存在 |
考点：估算无理数的大小
专题：
分析：由正方形的面积等于边长的平方，可得到a2=6，∵4＜6＜9，∴22＜a2＜32，即：2＜a＜3．
解答：解：∵正方形的面积等于边长的平方，
∴a2=6，
∵4＜6＜9，
∴22＜a2＜32，
即：2＜a＜3．
故选B．
∴a2=6，
∵4＜6＜9，
∴22＜a2＜32，
即：2＜a＜3．
故选B．
点评：本题考查了估算无理数的大小，解题的关键是找出和6左右最接近的两个能完全开方的数．
练习册系列答案
相关题目
一个直角三角形两直角边长分别为3和4，下列说法正确的是（ ）
| A、斜边长为25 | ||
| B、三角形的周长为25 | ||
C、斜边长上的高为
| ||
| D、三角形的面积为20 |
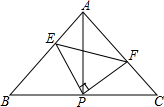如图所示，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E，F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），给出以下五个结论：①AE=CF；②△EPF是等腰直角三角形；③S四边形AEPF=