题目内容
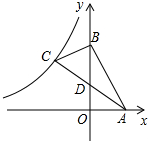 如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且
如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且| CD |
| AD |
| 7 |
| 6 |
| k |
| x |
考点:相似三角形的判定与性质,一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征
专题:常规题型
分析:作CE⊥x轴与E,构造出DO∥CE,根据
=
,求出C点横坐标,再根据BC与AB垂直,求出直线BC的比例系数,再利用B点坐标求出一次函数BC的解析式,将C点横坐标代入解析式,即可求出C点纵坐标,将C点横坐标代入反比例函数解析式即可得到k的值.
| CD |
| AD |
| 7 |
| 6 |
解答:解: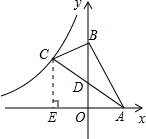 作CE⊥x轴与E.
作CE⊥x轴与E.
因为AB的解析式为y=-2x+6,则A点坐标为(3,0),B点坐标为(0,6),
∵
=
,
∴
=
,
∵DO∥CE,
∴
=
,
即
=
,
∴AE=
,
OE=
-3=
.
可知,C点横坐标为-4.
设BC解析式为y=dx+b,
∵BC⊥AB,
∴d=
,
得到函数解析式为y=
x+b,
将B(0,6)代入解析式得,b=6,
则BC的解析式为y=
x+6.
C点横坐标-
代入y=
x+6得,y=
×(-
)+6=
.
故C点坐标为(-
,
),
代入y=
得,k=-
.
故答案为-
.
 作CE⊥x轴与E.
作CE⊥x轴与E.因为AB的解析式为y=-2x+6,则A点坐标为(3,0),B点坐标为(0,6),
∵
| CD |
| AD |
| 7 |
| 6 |
∴
| AD |
| AC |
| 6 |
| 13 |
∵DO∥CE,
∴
| AO |
| AE |
| AD |
| AC |
即
| 3 |
| AE |
| 6 |
| 13 |
∴AE=
| 13 |
| 2 |
OE=
| 13 |
| 2 |
| 7 |
| 2 |
可知,C点横坐标为-4.
设BC解析式为y=dx+b,
∵BC⊥AB,
∴d=
| 1 |
| 2 |
得到函数解析式为y=
| 1 |
| 2 |
将B(0,6)代入解析式得,b=6,
则BC的解析式为y=
| 1 |
| 2 |
C点横坐标-
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 17 |
| 4 |
故C点坐标为(-
| 7 |
| 2 |
| 17 |
| 4 |
代入y=
| k |
| x |
| 119 |
| 8 |
故答案为-
| 119 |
| 8 |
点评:本题主要考查了反比例函数的性质、相互垂直的直线的比例系数的关系、待定系数法求反比例函数解析式等知识,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有人对某旅游区旅游的人数进行了10天的统计,结果有3天是每天800人,有2天是每天1200人,有5天是每天700人.若每月按30天计算,则每月大约有多少人来这个旅游区旅游( )
| A、22600人 |
| B、23500人 |
| C、24300人 |
| D、24900人 |
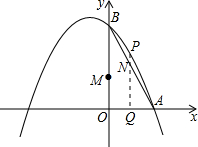 如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒. 如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是
如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是