题目内容
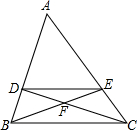 如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=
如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=考点:相似三角形的判定与性质
专题:常规题型
分析:易证△DEF∽△BCF,可得出DE:BC的值,再根据△ADE∽△ABC,可得AE和AC的比例,即可求出AE:EC的值.
解答:解:∵DE∥BC,
∴△DEF∽△BCF,△ADE∽△ABC
∴DE:BC=EF:BF,DE:BC=AE:AC
∴AE:AC=EF:BF=3:4,
∴AE:EC=3:(4-3)=3.
∴△DEF∽△BCF,△ADE∽△ABC
∴DE:BC=EF:BF,DE:BC=AE:AC
∴AE:AC=EF:BF=3:4,
∴AE:EC=3:(4-3)=3.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个直角三角形两直角边长分别为3和4,下列说法正确的是( )
| A、斜边长为25 | ||
| B、三角形的周长为25 | ||
C、斜边长上的高为
| ||
| D、三角形的面积为20 |
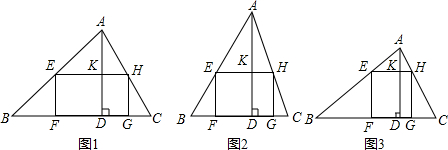
 如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是
如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是 如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.
如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.