题目内容
17.计算:(1)$\frac{2x-y}{x}$•$\frac{y}{y-2x}$
(2)$\frac{2a+6}{{a}^{2}-4a+4}$÷$\frac{a+3}{a-2}$
(3)($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)•$\frac{x}{4-x}$.
分析 (1)利用分式的基本性质即可求出答案
(2)先将分子分母进行因式分解,然后再约分
(3)先将分子分母进行因式分解,然后去括号进行化简运算.
解答 解:(1)原式=$\frac{2x-y}{x}$•$\frac{y}{-(2x-y)}$=-$\frac{y}{x}$
(2)原式=$\frac{2(a+3)}{{(a-2)}^{2}}$•$\frac{a-2}{a+3}$=$\frac{2}{a-2}$
(3)原式=($\frac{x+2}{x(x-2)}$-$\frac{x-1}{{(x-2)}^{2}}$)•$\frac{-x}{x-4}$
=$\frac{-(x+2)}{(x-2)(x-4)}$+$\frac{x(x-1)}{(x-2)^{2}(x-4)}$
=$-\frac{1}{{(x-2)}^{2}}$
点评 本题考查分式的混合运算,解题的关键是熟练运用分式的基本性质,本题属于基础题型.

练习册系列答案
相关题目
5.下列个数中,无理数是( )
| A. | 0 | B. | 0.1010010001 | C. | $\sqrt{3}$ | D. | -$\frac{1}{3}$ |
12.不能判定四边形ABCD是平行四边形的条件是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |
6.一个三角形三遍的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则该三角形的最短边是( )
| A. | 6 | B. | 9 | C. | 10 | D. | 15 |
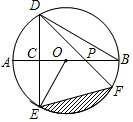 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.