题目内容
2.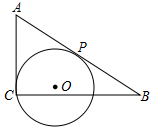 如图,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,则⊙O的半径r的最大值与最小值之差为( )
如图,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,则⊙O的半径r的最大值与最小值之差为( )| A. | $\frac{10}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{32}{15}$ | D. | $\frac{25}{12}$ |
分析 直接利用圆的切线性质分别得出⊙O的半径r的最大值与最小值,进而得出答案.
解答 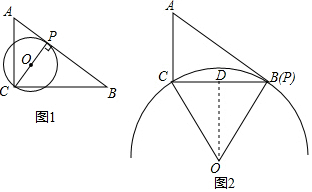 解:如图1,作CP⊥AB于点P,
解:如图1,作CP⊥AB于点P,
∵∠ACB=90°,AC=3,BC=4,
∴AB=5,
则AB•CP=AC•BC,
故5CP=3×4
解得:CP=$\frac{12}{5}$,
即半径最小值为:$\frac{6}{5}$,
如图2,当P与B重合时,圆最大.O在BC的垂直平分线上,过O作OD⊥BC于D,
由BD=$\frac{1}{2}$BC=2,
∵AB是切线,
∴∠ABO=90°,
∴∠ABD+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴$\frac{BD}{OB}$=sin∠BOD=sin∠ABC=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴OB=$\frac{10}{3}$,即半径最大值为$\frac{10}{3}$,
⊙O的半径r的最大值与最小值之差为:$\frac{10}{3}$-$\frac{6}{5}$=$\frac{32}{15}$.
故选:C.
点评 此题主要考查了切线的性质以及勾股定理等知识,正确掌握切线的性质是解题关键.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
13.下列说法不正确的是( )
| A. | 最大的负整数为-1 | B. | 最小的正整数为1 | ||
| C. | 最小的整数是0 | D. | 相反数等于它本身的数是0 |
10.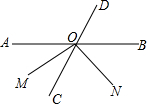 如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
 如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
12.不能判定四边形ABCD是平行四边形的条件是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |
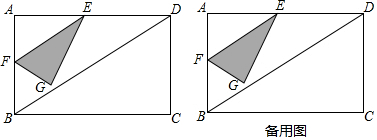
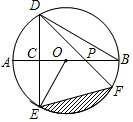 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.