题目内容
20.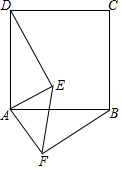 如图,正方形ABCD内一点E,△ADE绕点A顺时针旋转能与△ABF重合,若AE=3,求∠EAF的度数和EF的长.
如图,正方形ABCD内一点E,△ADE绕点A顺时针旋转能与△ABF重合,若AE=3,求∠EAF的度数和EF的长.
分析 根据旋转的性质,可得∠DAE=∠BAF,AE=AF,再根据正方形ABCD中,∠DAB=90°,即可得出∠EAF=90°,运用勾股定理即可得出EF的长.
解答 解:由题可得,△ADE≌△ABF,
∴∠DAE=∠BAF,AE=AF,
∵正方形ABCD中,∠DAB=90°,
∴∠EAF=90°,
∵AE=3,
∴由勾股定理可得,EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{18}$=3$\sqrt{2}$.
点评 本题主要考查了旋转的性质,勾股定理以及正方形的性质的运用,解题时注意:旋转前、后的图形全等.

练习册系列答案
相关题目
10.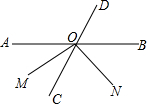 如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
 如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )
如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
15.点P(3,5)关于原点中心对称的点的坐标是( )
| A. | (5,3) | B. | (-3,5) | C. | (3,-5) | D. | (-3,-5) |
5.下列个数中,无理数是( )
| A. | 0 | B. | 0.1010010001 | C. | $\sqrt{3}$ | D. | -$\frac{1}{3}$ |
12.不能判定四边形ABCD是平行四边形的条件是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |