Question

13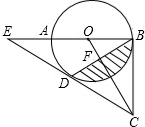．已知：如图，AB是⊙O的直径，BC切⊙O于点B，D为⊙O上一点，CD=CB，延长CD交BA的延长线于点E．
（1）求证：CD是⊙O的切线；
（2）连接OC，交BD于点F，若OF=2，∠E=30°，求图中阴影部分的面积（结果保留π）．

Answer 1

分析 （1）连接OD，可以得到∠BDC=∠DBC，∠ODB=∠OBD，进而得出∠ODC=∠OBC=90°，据此即可得出证明；
（2）可以先求出∠BOD的度数，由OD=OB，CD=CB，可以证明OC是线段BD的垂直平分线，进而求出OD的长，据此即可得解．

解答 解：（1）如图，连接OD，
∵AB是⊙O的直径，BC切⊙O于点B，
∴∠OBC=90°，
∵OD=OB，∴∠ODB=∠OBD，
∵CD=CB，∴∠BDC=∠DBC，
∴∠BDC+∠ODB=∠DBC+∠OBD，
即：∠ODC=∠OBC=90°，
∴CD是⊙O的切线；

                   
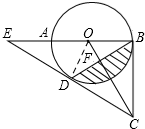
（2）由（1）知，∠ODE=∠ODC，
∵∠E=30°，∴∠EOD=60°，
∴∠DOB=180°-60°=120°，
∵OD=OB，CD=CB，
∴OC是线段BD的垂直平分线，
∴∠ODF=$\frac{1}{2}$∠DOB=$\frac{1}{2}$×120°=60°，
在Rt△OFD中，OF=2，
∴OD=$\frac{2}{cos60°}$=4，DF=2$\sqrt{3}$，
∴DB=4$\sqrt{3}$，
S_阴影=S_扇形ODB-S_△ODB
=$\frac{120•π•{4}^{2}}{360}$-$\frac{1}{2}×4\sqrt{3}×2$
=$\frac{16π}{3}$-$4\sqrt{3}$．

点评 本题主要考查了圆的切线的性质与切线的判定，还考查了扇形面积公式，三角形的面积公式等知识点，是基础题目，要注意总结．