题目内容
1. 如图,正方形ABCD,请你用图中的字母a、b写出三个形式不同的表示它面积的代数式.
如图,正方形ABCD,请你用图中的字母a、b写出三个形式不同的表示它面积的代数式.
分析 (1)大正方形的边长等于a+b,所以面积为(a+b)2;
(2)大正方形的面积正好等于两个小正方形和两个长方形的面积之和.因为两个长方形是相同的,所以两个长方形的面积之和=ab×2=2ab.两个小正方形面积=a2+b2;
(3)大正方形的面积也可分为两个小长方形的面积和即:(a+b)a+(a+b)b.
解答 解:(1)大正方形的边长等于a+b,所以面积为(a+b)2;
(2)大正方形的面积正好等于两个小正方形和两个长方形的面积之和.
因为两个长方形是相同的,所以两个长方形的面积之和=ab×2=2ab.
两个小正方形面积=a2+b2;
即:a2+b2+2ab;
(3)大正方形的面积也可分为两个小长方形的面积和即:(a+b)a+(a+b)b.
故三个形式不同的表示它面积的代数式可以是:(a+b)2;a2+b2+2ab;(a+b)a+(a+b)b.
点评 本题考查了列代数式解决实际问题(图形的面积)解题的关键是将正方形分割为不同的小正方形或长方形再分别求出即可.

练习册系列答案
相关题目
20.方程2x-1=3x+2的解为( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
1.一个多边形的外角和是内角和的$\frac{2}{5}$,这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18. 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )| A. | -6 | B. | -5 | C. | 6 | D. | 5 |
 在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是26.
在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是26. (1)第1列第5行的数是25,第5列第1行的数是17
(1)第1列第5行的数是25,第5列第1行的数是17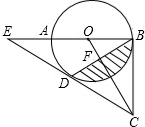 已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.
已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E. 如图,已知平行四边形ABCD的周长为20,对角线AC,BD相交于点O,过O作EO⊥AC,连接EC,则△DEC的周长为10.
如图,已知平行四边形ABCD的周长为20,对角线AC,BD相交于点O,过O作EO⊥AC,连接EC,则△DEC的周长为10. 已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.
已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.