题目内容
18.四边形ABCD为菱形,点P为对角线BD上的一个动点.
(1)如图1,连接AP并延长交BC的延长线于点E,连接 PC,求证:∠AEB=∠PCD.
(2)如图1,当PA=PD且PC⊥BE时,求∠ABC的度数.
(3)连接AP并延长交射线BC于点E,连接 PC,若∠ABC=90°且△PCE是等腰三角形,求∠PEC的度数.
分析 (1)利用菱形的性质,易得∠PDA=∠PDC,AD=CD,利用SAS定理证得△PAD≌△PCD,由全等三角形的性质及平行线的性质得到结论;
(2)方法一,首先利用等腰三角形的性质得∠PAD=∠PDA,设∠PAD=∠PDA=x,利用外角性质易得∠BPC=2x,因为PC⊥BE,得x,得∠ABC的度数;方法二,利用平行线的性质易得CM⊥AD,由全等三角形的判定得△PAM≌△PDM,得AM=DM,由垂直平分线的性质得AC=CD=BC=AB,得△ABC是等边三角形,得∠ABC的度数;
(3)分类讨论:①当点E在BC的延长线上时,首先利用等腰三角形的性质得CP=CE,易得∠BCP=∠CPE+∠CEP=2∠CEP,由正方形的性质得∠PBA=∠PBC=45°,由全等三角形的判定得△ABP≌△CBP,易得∠BAP=∠BCP=2∠CEP,因为∠BAP+∠PEC=90°,求得∠PEC的度数;②当点E在BC上时,同理得出结论.
解答 (1)证明:∵四边形ABCD是菱形,
∴∠PDA=∠PDC,AD=CD AD∥BC,
在△PAD与△PCD中,
$\left\{\begin{array}{l}{AD=CD}\\{∠PDA=∠PDC}\\{PD=PD}\end{array}\right.$,
∴△PAD≌△PCD(SAS),
∴∠PAD=∠PCD,
又∵AD∥BC,
∴∠AEB=∠PAD=∠PCD;
(2)解:如图1,
(方法一)∵PA=PD,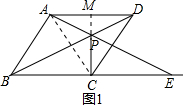
∴∠PAD=∠PDA,
设∠PAD=∠PDA=x,则∠BPC=∠PDC+∠PCD=∠PDA+∠PAD=2x
∵PC⊥BE
∴2x+x=90°,
∴x=30°,
∴∠ABC=2x=60°;
(方法二):延长CP交AD于M,
∵AD∥BC,PC⊥BC,
∴CM⊥AD
∵PA=PD,
∴△PAM≌△PDM (HL),
∴AM=DM,
∴CM垂直平分AD
连接AC,则AC=CD=BC=AB,
∴△ABC是等边三角形,
∴∠ABC=60°;
(3)解:①当点E在BC的延长线上时,如图2,△PCE是等腰三角形,则CP=CE,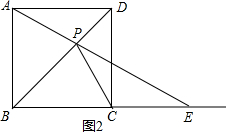
∴∠BCP=∠CPE+∠CEP=2∠CEP
∵四边形ABCD是菱形,∠ABC=90°,
∴菱形ABCD是正方形,
∴∠PBA=∠PBC=45°,
在△ABP与△CBP中,
$\left\{\begin{array}{l}{AB=CB}\\{∠PBA=∠PBC}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP
∵∠BAP+∠PEC=90°,2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,如图3,△PCE是等腰三角形,则PE=CE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,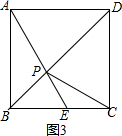
∵四边形ABCD是菱形,∠ABC=90°
∴菱形ABCD是正方形,
∴∠PBA=∠PBC=45°,又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,2∠BCP+∠BCP=90°
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°-∠AEB=120°,
综上所述:∠PEC=30°或∠PEC=120°.
点评 本题主要考查了菱形的性质和正方形的性质,全等三角形的判定及性质,数形结合,利用方程思想和分类讨论是解答此题的关键.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | -5 | B. | 0 | C. | π | D. | 3 |
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )| A. | -6 | B. | -5 | C. | 6 | D. | 5 |
 (1)第1列第5行的数是25,第5列第1行的数是17
(1)第1列第5行的数是25,第5列第1行的数是17(2)请用含n(n为正整数)的代数式,表示数表中第n行第1列的数,n2和第n行第n列的数n2-n+1
(3)根据规律直接写出第9行第8列的数73.
| A. | $\frac{1}{2014}$ | B. | -$\frac{1}{2014}$ | C. | 2014 | D. | -2014 |
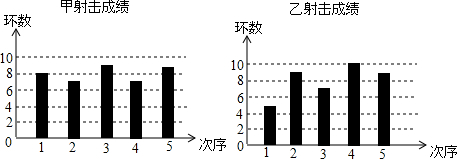
以下关于甲乙射击成绩的比较,正确的是( )
| A. | 甲的中位数较大,方差较小 | B. | 甲的中位数较小,方差较大 | ||
| C. | 甲的中位数和方差都比乙小 | D. | 甲的中位数和方差都比乙大 |
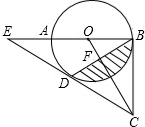 已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.
已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E. 如图,已知平行四边形ABCD的周长为20,对角线AC,BD相交于点O,过O作EO⊥AC,连接EC,则△DEC的周长为10.
如图,已知平行四边形ABCD的周长为20,对角线AC,BD相交于点O,过O作EO⊥AC,连接EC,则△DEC的周长为10.