题目内容
12.(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”或“列表”等方式给出分析过程)(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是$\frac{n-1}{{n}^{2}}$(请直接写出结果).
分析 (1)根据画树状图,可得总结果与传到甲手里的情况,根据传到甲手里的情况比上总结过,可得答案;
(2)根据第一步传的结果是n,第二步传的结果是n2,第三步传的结果是总结过是n3,传给甲的结果是n(n-1),根据概率的意义,可得答案.
解答 解:(1)画树状图:
共有9种等可能的结果,其中符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=$\frac{3}{9}$=$\frac{1}{3}$.
(2)第三步传的结果是n3,传给甲的结果是n(n-1),
第三次传球后球回到甲手里的概率是$\frac{n(n-1)}{{n}^{3}}$=$\frac{n-1}{{n}^{2}}$,
故答案为:$\frac{n-1}{{n}^{2}}$.
点评 本题考查了树状图法计算概率,计算概率的方法有树状图法与列表法,画树状图是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.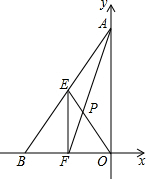 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )| A. | (-1,$\frac{4}{3}$) | B. | (-$\frac{3}{2}$,2) | C. | (-$\frac{3}{2}$,$\frac{4}{3}$) | D. | (-1,2) |
20.方程2x-1=3x+2的解为( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
17.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | π | D. | 3 |
4.下列各组线段能构成直角三角形的一组是( )
| A. | 30,40,50 | B. | 7,12,13 | C. | 5,9,12 | D. | 3,4,6 |
1.一个多边形的外角和是内角和的$\frac{2}{5}$,这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于16cm.
如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于16cm.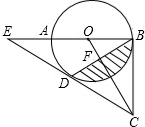 已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.
已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.