题目内容
3.已知:点A、B是⊙O上的两个定点,且∠AOB=80°,P是⊙O上不与A、B重合的一个动点,∠APB的度数是40°或140°.分析 分类讨论:当点P在优弧AB上时,根据圆周角定理易得∠APB=$\frac{1}{2}$∠AOB=40°;当点P在弧AB上时,即P′点的位置,根据圆内接四边形的性质易得则∠P′=140°,于是得到∠APB的度数为40°或140°.
解答 解: 如图,
如图,
当点P在优弧AB上时,∠APB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×80°=40°;
当点P在弧AB上时,即P′点的位置,则∠P′=180°-∠P=140°,
综上所述,∠APB的度数为40°或140°.
故答案为40°或140°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
18.一种细胞的直径约为1.6×10-6米,那么它的一百万倍相当于( )
| A. | 一元硬币的直径 | B. | 数学课本宽度 | ||
| C. | 五层楼房的高度 | D. | 初中学生小丽的身高 |
8.甲、乙两名队员在5次设计测试中,命中环数的平均数都是8环,各次成绩分别如下: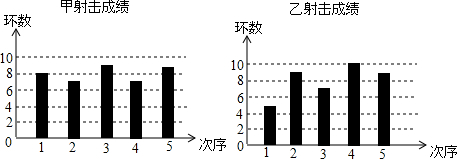
以下关于甲乙射击成绩的比较,正确的是( )

以下关于甲乙射击成绩的比较,正确的是( )
| A. | 甲的中位数较大,方差较小 | B. | 甲的中位数较小,方差较大 | ||
| C. | 甲的中位数和方差都比乙小 | D. | 甲的中位数和方差都比乙大 |
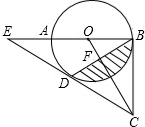 已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.
已知:如图,AB是⊙O的直径,BC切⊙O于点B,D为⊙O上一点,CD=CB,延长CD交BA的延长线于点E.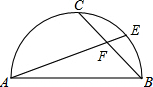 如图,AB是半圆的直径,点C是弧AB的中点,点E是弧BC的中点,连结AE、BC交于点F,则$\frac{EF}{AF}$的值为$\frac{\sqrt{2}-1}{2}$.
如图,AB是半圆的直径,点C是弧AB的中点,点E是弧BC的中点,连结AE、BC交于点F,则$\frac{EF}{AF}$的值为$\frac{\sqrt{2}-1}{2}$. 已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.
已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.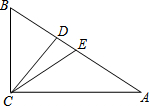 在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b
在直角三角形ABC中,CD、CE分别是斜边AB上的高、中线,BC=a,AC=b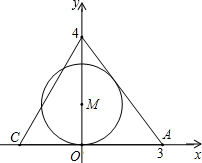 如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.
如图,直角坐标系中,点A(3,0)、B(0,4)分别位于x轴和y轴上,点C在x轴的负半轴上,且∠ACB=60°,在y轴正半轴上有一点M,以M为圆心,MO为半径作⊙M与BA相切,若保持圆的大小不变,△ABC位置不变,将⊙M向右平移$\frac{\sqrt{3}}{6}$个单位,⊙M与BC相切.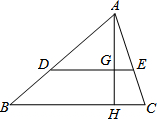 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.
如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若$\frac{AG}{GH}=\frac{3}{2}$,则$\frac{DE}{BC}$=$\frac{3}{5}$.